题目内容
函数f(x)=(
) x2+2(a-1)x+2在区间(-∞,4]上单调递增,那么实数a的取值范围是( )
| 1 |
| 2 |
| A、a≤-3 | B、a≥-3 |
| C、a≤5 | D、a≥5 |
考点:指数函数单调性的应用
专题:函数的性质及应用
分析:根据复函函数单调性同增异减的原则,和指数函数的单调性,可得y=x2+2(a-1)x+2区间(-∞,4]上单调递单调递减,求二次函数的对称轴,利用对称轴和单调区间的关系,建立条件关系即可.
解答:
解:∵数f(x)=(
) x2+2(a-1)x+2在区间(-∞,4]上单调递增,
∴y=x2+2(a-1)x+2区间(-∞,4]上单调递单调递减,
函数f(x)=x2+2(a-1)x+2的图象开口朝上,且对称轴为x=1-a,
要使函数f(x)在区间(-∞,4]上单调递增,
则4≤1-a,即a≤-3.
故选:A.
| 1 |
| 2 |
∴y=x2+2(a-1)x+2区间(-∞,4]上单调递单调递减,
函数f(x)=x2+2(a-1)x+2的图象开口朝上,且对称轴为x=1-a,
要使函数f(x)在区间(-∞,4]上单调递增,
则4≤1-a,即a≤-3.
故选:A.
点评:本题主要考查指数函数和二次函数的图象和性质,复函函数单调性同增异减的原则,利用对称轴和单调区间之间的关系是解决本题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
若2014a=
,2014b=3,则a+2b等于( )
| 2014 |
| 9 |
| A、0 | B、1 | C、2 | D、3 |
等比数列{an}中,已知a3•a10=8a52,a2=2,则a1=( )
| A、2 | ||
B、
| ||
C、
| ||
| D、1 |
定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期为π,且当x∈[-
,0)时,f(x)=sin x,则f(-
)的值为( )
| π |
| 2 |
| 2π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
若从1,2,3,4,5,6,7,8,9,10这10个数中任意取出3个数,则这三个数互不相邻的取法种数有( )
| A、20种 | B、56种 |
| C、60种 | D、120种 |
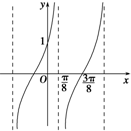 已知函数f(x)=Atan(ωx+ϕ)(
已知函数f(x)=Atan(ωx+ϕ)(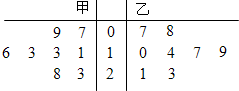 某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.