题目内容
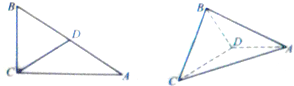 在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD.
在Rt△ABC中,BC=2,AB=4,∠ACB=90°,D为边AB的中点,沿CD把△BCD折起,使平面BCD⊥平面ACD.(1)求异面直线BC与AD所成角的余弦值.
(2)求平面ABC与平面ABD所成的锐二面角的余弦值.
考点:二面角的平面角及求法,异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
分析:(1)在平面ACD中,过F作CF∥AD,且CF=AD=2,连接BF,则∠BCF或补角即为异面直线BC和AD所成的角.过B在平面BCD内作BE⊥CD,则垂足E即为中点,即有BE=
,再由余弦定理求EF,由勾股定理得到BF,再由余弦定理即可得到所求值;
(2)取AB的中点H,连接DH,则DH⊥AB,过D作DO⊥平面ABC,垂足为O,连接OH,易得OH⊥AB,则∠DHO即为面ABC与面ABD所成的锐二面角的平面角,在△ABD中求得DH,设D到平面ABC的距离为d,由于VD-ABC=VB-ACD,即有
dS△ABC=
BE•S△ACD,通过计算即可得到d,再在△DHO中,运用正弦和余弦函数的定义,即可得到所求值.
| 3 |
(2)取AB的中点H,连接DH,则DH⊥AB,过D作DO⊥平面ABC,垂足为O,连接OH,易得OH⊥AB,则∠DHO即为面ABC与面ABD所成的锐二面角的平面角,在△ABD中求得DH,设D到平面ABC的距离为d,由于VD-ABC=VB-ACD,即有
| 1 |
| 3 |
| 1 |
| 3 |
解答:
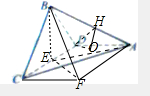 解:(1)在平面ACD中,过F作CF∥AD,且CF=AD=2,连接BF,
解:(1)在平面ACD中,过F作CF∥AD,且CF=AD=2,连接BF,
则∠BCF或补角即为异面直线BC和AD所成的角.
过B在平面BCD内作BE⊥CD,则垂足E即为中点,
即有BE=
,由于平面BCD⊥平面ACD,则BE⊥平面ACD,
则有BE⊥EF,
在△CEF中,CE=1,CF=2,∠ECF=60°,
则EF2=1+4-2×1×2×cos60°=3,
即有BF2=BE2+EF2=3+3=6,
即有cos∠BCF=
=
,
故异面直线BC与AD所成角的余弦值为
;
(2)取AB的中点H,连接DH,则DH⊥AB,
过D作DO⊥平面ABC,垂足为O,连接OH,易得OH⊥AB,
则∠DHO即为面ABC与面ABD所成的锐二面角的平面角,
连接AE,则BE⊥AE,即有AB2=AE2+BE2=3+1+4-2×1×2×(-
)=10,
在△ABD中,DH=
=
=
,
设D到平面ABC的距离为d,
在△ABC中,BC=2,AC=2
,AB=
,
由余弦定理得,cos∠ABC=
,即有sin∠ABC=
,
则△ABC的面积为
×
×2×
=
,
由于VD-ABC=VB-ACD,即有
dS△ABC=
BE•S△ACD,
即
d×
=
×
×
×2×2×
,解得d=
,
则有sin∠DHO=
=
×
=
,
即有cos∠DHO=
.
故平面ABC与平面ABD所成的锐二面角的余弦值为
.
 解:(1)在平面ACD中,过F作CF∥AD,且CF=AD=2,连接BF,
解:(1)在平面ACD中,过F作CF∥AD,且CF=AD=2,连接BF,则∠BCF或补角即为异面直线BC和AD所成的角.
过B在平面BCD内作BE⊥CD,则垂足E即为中点,
即有BE=
| 3 |
则有BE⊥EF,
在△CEF中,CE=1,CF=2,∠ECF=60°,
则EF2=1+4-2×1×2×cos60°=3,
即有BF2=BE2+EF2=3+3=6,
即有cos∠BCF=
| 4+4-6 |
| 2×2×2 |
| 1 |
| 4 |
故异面直线BC与AD所成角的余弦值为
| 1 |
| 4 |
(2)取AB的中点H,连接DH,则DH⊥AB,
过D作DO⊥平面ABC,垂足为O,连接OH,易得OH⊥AB,
则∠DHO即为面ABC与面ABD所成的锐二面角的平面角,
连接AE,则BE⊥AE,即有AB2=AE2+BE2=3+1+4-2×1×2×(-
| 1 |
| 2 |
在△ABD中,DH=
| BD2-BH2 |
4-
|
| ||
| 2 |
设D到平面ABC的距离为d,
在△ABC中,BC=2,AC=2
| 3 |
| 10 |
由余弦定理得,cos∠ABC=
| 1 | ||
2
|
| ||
2
|
则△ABC的面积为
| 1 |
| 2 |
| 10 |
| ||
2
|
| ||
| 2 |
由于VD-ABC=VB-ACD,即有
| 1 |
| 3 |
| 1 |
| 3 |
即
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 6 | ||
|
则有sin∠DHO=
| DO |
| DH |
| 6 | ||
|
| 2 | ||
|
2
| ||
|
即有cos∠DHO=
| ||
| 13 |
故平面ABC与平面ABD所成的锐二面角的余弦值为
| ||
| 13 |
点评:本题考查空间直线与平面的位置关系,考查空间的异面直线所成的角和二面角的求法,考查运算能力和空间想象能力,属于中档题.

练习册系列答案
相关题目
定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期为π,且当x∈[-
,0)时,f(x)=sin x,则f(-
)的值为( )
| π |
| 2 |
| 2π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
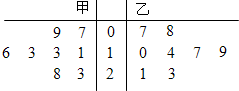 某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.
某篮球队甲、乙两名队员在本赛季已结束的8场比赛中得分统计的茎叶图如图:若以甲、乙两名队员得分的频率作为概率,假设甲、乙两名队员在同一场比赛中的得分互不影响.