题目内容
11.设曲线y=1nx在x=2处的切线与直线ax+y+1=0垂直,则a的值为( )| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
分析 求出函数y=1nx的导函数,得到函数在x=2处的导数值,再由两线垂直与斜率的关系列式求得a值.
解答 解:由y=1nx,得y′=$\frac{1}{x}$,
∴$y′{|}_{x=2}=\frac{1}{2}$,
∵曲线y=1nx在x=2处的切线与直线ax+y+1=0垂直,
∴-a$•\frac{1}{2}=-1$,则a=2.
故选:A.
点评 本题考查利用导数研究过去线上某点处的切线方程,函数在曲线上某点处的导数,就是函数在该点处的导数值,是中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
1.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=3,且$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为$\frac{π}{4}$,则|$\overrightarrow{b}$|=( )
| A. | 6 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
6.已知公差不为0的等差数列{an}与等比数列$\{{b_n}\},{a_1}=2,{b_n}={a_{2^n}}$,则{bn}的前5项的和为( )
| A. | 142 | B. | 124 | C. | 128 | D. | 144 |
3.已知函数f(x)=1n(x+2)+1n(x-2),则f(x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 非奇非偶函数 |
20.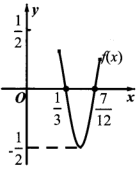 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
 函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )
函数f(x)=$\frac{1}{2}$sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)的单调递增区间为( )| A. | $(-\frac{1}{24}+2kπ,\frac{5}{24}+2kπ)$,(k∈Z) | B. | $(-\frac{1}{12}+\frac{k}{2},\frac{5}{12}+\frac{k}{2})$,(k∈Z) | ||
| C. | $(-\frac{1}{12}+2kπ,\frac{1}{3}+2kπ)$,(k∈Z) | D. | $(-\frac{1}{24}+\frac{k}{2},\frac{5}{24}+\frac{k}{2})$,(k∈Z) |
1.执行如图所示的程序框图,若输入a=-7,d=3,则输出的S为( )


| A. | S=-12 | B. | S=-11 | C. | S=-10 | D. | S=-6 |
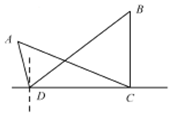 如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.
如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.