题目内容
如果二次函数f(x)=ax2+bx+c对任意实数x都有f(2-x)=f(x)成立,且f(accsin
)>f(arccos
),则a-2014b的符号是( )
| 2 |
| 3 |
| 3 |
| 4 |
| A、大于零 | B、小于零 |
| C、等于零 | D、不能确定 |
考点:二次函数的性质
专题:函数的性质及应用,三角函数的求值
分析:本题可以先利用f(2-x)=f(x)得到参数a、b的一个相等关系,再利用f(accsin
)>f(arccos
)得到a、b的取值范围,然后研究a-2014b,得到值的正负,得到本题结论.
| 2 |
| 3 |
| 3 |
| 4 |
解答:
解:∵二次函数f(x)=ax2+bx+c对任意实数x都有f(2-x)=f(x)成立,
∴f(1+x)=f[2-(1+x)]=f(1-x),
∴函数图象的对称轴方程为x=1.
∴-
=1,即b=-2a.
则有:a-2014b=a+4028a=4029a.
记accsin
=α,arcccos
=β,
则有sinα=
,cosβ=
,且α∈(0,
),β∈(0,
)
∴sinβ=
.
∵
>
,
∴α>β,即accsin
>arcccos
,
∵sin1≈0.8414,0.8414>
,
∴1>α>β.
∵f(accsin
)>f(arccos
),即f(α)>f(β),
∴函数f(x)在(1,+∞)单调递增,
∴a>0.
∴a-2014b=a+4028a=4029a>0.
故选A.
∴f(1+x)=f[2-(1+x)]=f(1-x),
∴函数图象的对称轴方程为x=1.
∴-
| b |
| 2a |
则有:a-2014b=a+4028a=4029a.
记accsin
| 2 |
| 3 |
| 3 |
| 4 |
则有sinα=
| 2 |
| 3 |
| 3 |
| 4 |
| π |
| 2 |
| π |
| 2 |
∴sinβ=
| ||
| 4 |
∵
| 2 |
| 3 |
| ||
| 4 |
∴α>β,即accsin
| 2 |
| 3 |
| 3 |
| 4 |
∵sin1≈0.8414,0.8414>
| 2 |
| 3 |
∴1>α>β.
∵f(accsin
| 2 |
| 3 |
| 3 |
| 4 |
∴函数f(x)在(1,+∞)单调递增,
∴a>0.
∴a-2014b=a+4028a=4029a>0.
故选A.
点评:本题考查了二次函数的对称轴、单调性,反三角函数值的比较,本题难度适中,有一定的综合性,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知直线Ax+By+C=0不经过第一象限,且A,B,C均不为零,则有( )
| A、C<0 | B、AB<0 |
| C、ABC<0 | D、AC>0 |
若0<α<
,则经过两点P1(0,cosα),P2(sinα,0)的直线的倾斜角为( )
| π |
| 2 |
| A、α$ | ||
B、
| ||
| C、π-α | ||
| D、-α |
在正方体EF⊥A1D中,A1D∥B1C分别为AB、BC中点,则异面直线EF与AB1所成角的余弦值为( )
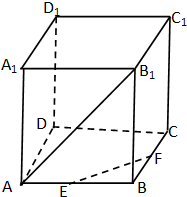

A、
| ||||
B、
| ||||
C、
| ||||
D、
|