Question

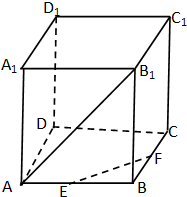
在正方体EF⊥A₁D中，A₁D∥B₁C分别为AB、BC中点，则异面直线EF与AB₁所成角的余弦值为（　　）

• A、

  3

  2

• B、

  3

  3

• C、

  2

  2

• D、

  1

  2

Answer 1

考点：异面直线及其所成的角

专题：计算题,空间角

分析：由题意，连接AC，B₁C，则△AB₁C是等边三角形，∠B₁AC=60°，确定∠B₁AC就是异面直线EF与AB₁所成角，即可得出结论．

解答： 解：由题意，连接AC，B₁C，则△AB₁C是等边三角形，∠B₁AC=60°，
∵E，F分别为AB、BC中点，
∴EF∥AC，
∴∠B₁AC就是异面直线EF与AB₁所成角，余弦值为

1

2

，
故选：D．

点评：本题考查异面直线及其所成的角，考查学生的计算能力，比较基础．