题目内容
4.已知函数f(x)=ex+ln(x+1)的图象在(0,f(0))处的切线与直线x-ny+4=0垂直,则n的值为-2.分析 由求导公式和法则求出函数的导数,由直线垂直的条件求出切线的斜率,即可求出n的值.
解答 解:依题意得,f′(x)=ex+$\frac{1}{x+1}$,所以f′(0)=2.
显然n≠0,直线x-ny+4=0的斜率为$\frac{1}{n}$,所以$\frac{1}{n}•2=-1$,解得n=-2,
故答案为:-2.
点评 本题考查了求导公式和法则,由导数的几何意义求切线方程,以及直线垂直的条件等,熟练掌握公式是解题的关键.

练习册系列答案
相关题目
16.当$x=\frac{π}{4}$时,函数f(x)=sin(ωx+φ)(A>0)取得最小值,则函数$y=f({\frac{3π}{4}-x})$是( )
| A. | 奇函数且图象关于点$({\frac{π}{2},0})$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于直线$x=\frac{π}{2}$对称 | D. | 偶函数且图象关于点$({\frac{π}{2},0})$对称 |
14.已知F1,F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1的直线l与E的左支交于P,Q两点,若|PF1|=2|F1Q|,且F2Q⊥PQ,则E的离心率是( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{17}}{3}$ |
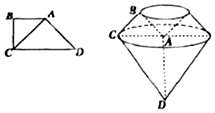 已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.
已知梯形ABCD中,AB∥CD,∠B=$\frac{π}{2}$,DC=2AB=2BC=2$\sqrt{2}$,以直线AD为旋转轴旋转一周的都如图所示的几何体.