题目内容
16.当$x=\frac{π}{4}$时,函数f(x)=sin(ωx+φ)(A>0)取得最小值,则函数$y=f({\frac{3π}{4}-x})$是( )| A. | 奇函数且图象关于点$({\frac{π}{2},0})$对称 | B. | 偶函数且图象关于点(π,0)对称 | ||
| C. | 奇函数且图象关于直线$x=\frac{π}{2}$对称 | D. | 偶函数且图象关于点$({\frac{π}{2},0})$对称 |
分析 由条件求得φ=2kπ-$\frac{π}{2}$-$\frac{π}{4}$ω,可得y=f($\frac{3π}{4}$-x)=-sinx,从而得出结论.
解答 解:由题意可得f($\frac{π}{4}$)=sin($\frac{π}{4}$ω+φ)=-1,∴$\frac{π}{4}$ω+φ=2kπ-$\frac{π}{2}$,k∈Z,
∴φ=2kπ-$\frac{π}{2}$-$\frac{π}{4}$ω,∴f(x)=sin(ωx+2kπ-$\frac{π}{2}$-$\frac{π}{4}$ω)=sin(ωx-$\frac{π}{2}$-$\frac{π}{4}$ω),
令ω=1,故函数y=f($\frac{3π}{4}$-x)=-sinx,
故它是奇函数且图象关于直线x=$\frac{π}{2}$对称,
故选:C.
点评 本题主要考查正弦函数的图象特征,求得y=f($\frac{3π}{4}$-x)的解析式,是解题的关键,属于基础题.

练习册系列答案
相关题目
7.已知$\frac{sinα-2cosα}{2sinα+3cosα}=2$,那么tanα的值为( )
| A. | -2 | B. | $-\frac{8}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
1.在△ABC中,A、B、C所对的边分别是a、b、c,已知a2+b2=c2+$\sqrt{3}$ab,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
8.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
6.在△ABC中,若B=2A,$a:b=1:\sqrt{3}$,则A=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
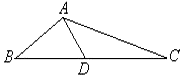 如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$
如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$