题目内容
19.已知函数$f(x)=sin2x+2{sin^2}\frac{1}{2}x$,则$f(\frac{π}{2017})+f(\frac{2π}{2017})+f(\frac{3π}{2017})+…+f(\frac{2016π}{2017})$=2016.分析 推导出f(π-x)+f(x)=2,由此能求出$f(\frac{π}{2017})+f(\frac{2π}{2017})+f(\frac{3π}{2017})+…+f(\frac{2016π}{2017})$的值.
解答 解:∵$f(x)=sin2x+2{sin^2}\frac{1}{2}x=2sinxcosx+1-cosx$,
f(π-x)=2sin(π-x)cos(π-x)+1-cos(π-x)=-2sinxcosx+1+cosx,
∴f(π-x)+f(x)=2,
∴$f({\frac{π}{2017}})+f({\frac{2π}{2017}})+f({\frac{3π}{2017}})$$+…+f({\frac{2016π}{2017}})=2×1008=2016$.
故答案为:2016.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知椭圆与双曲线$\frac{x^2}{3}-\frac{y^2}{2}=1$有共同的焦点,且离心率为$\frac{{\sqrt{5}}}{5}$,则椭圆的标准方程为( )
| A. | $\frac{x^2}{20}+\frac{y^2}{25}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{5}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{20}=1$ | D. | $\frac{x^2}{5}+\frac{y^2}{25}=1$ |
7.已知$\frac{sinα-2cosα}{2sinα+3cosα}=2$,那么tanα的值为( )
| A. | -2 | B. | $-\frac{8}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
14.已知$sinα-2cosα=\frac{{\sqrt{10}}}{2}$,则tan2α=( )
| A. | $\frac{4}{3}$ | B. | $-\frac{3}{4}$ | C. | $\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
8.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
9.已知集合U=R(R是实数集),A={x|-1≤x≤1},B={x|x2-2x<0},则A∪(∁UB)=( )
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
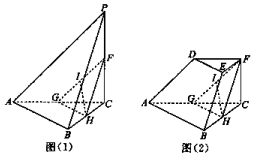 如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.
如图(1),三棱锥P-ABC中,PC⊥平面ABC,F,G,H,分别是PC,AC,BC的中点,I是线段FG上任意一点,PC=AB=2BC,过点F作平行于底面ABC的平面截三棱锥,得到几何体DEF-ABC,如图(2)所示.