题目内容
14.已知F1,F2是双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,过点F1的直线l与E的左支交于P,Q两点,若|PF1|=2|F1Q|,且F2Q⊥PQ,则E的离心率是( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{\sqrt{15}}{3}$ | D. | $\frac{\sqrt{17}}{3}$ |
分析 可设|F1Q|=m,可得|PF1|=2m,由双曲线定义可得|PF2|-|PF1|=2a,|QF2|-|QF1|=2a,求得|PF2|=2a+2m,|QF2|=m+2a,再分别在直角三角形PQF2中,直角三角形F1QF2中,运用勾股定理和离心率公式,化简整理,即可得到所求值.
解答 解:若|PF1|=2|F1Q|,且F2Q⊥PQ,
可设|F1Q|=m,可得|PF1|=2m,
由双曲线定义可得|PF2|-|PF1|=2a,
|QF2|-|QF1|=2a,
即有|PF2|=2a+2m,
|QF2|=m+2a,
在直角三角形PQF2中,
可得|PQ|2+|QF2|2=|PF2|2,
即为(3m)2+(m+2a)2=(2a+2m)2,
化简可得2a=3m,即m=$\frac{2}{3}$a,
再由直角三角形F1QF2中,
可得|F2Q|2+|QF1|2=|F1F2|2,
即为(2a+m)2+m2=(2c)2,
即为$\frac{64}{9}$a2+$\frac{4}{9}$a2=4c2,
即$\frac{17}{9}$a2=c2,
由e=$\frac{c}{a}$=$\frac{\sqrt{17}}{3}$.
故选:D.
点评 本题考查双曲线的定义、方程和性质,主要是求双曲线的离心率,注意运用定义法和直角三角形的勾股定理,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
2.已知0<c<1,a>b>1,下列不等式成立的是( )
| A. | ca>cb | B. | $\frac{a}{a-c}>\frac{b}{b-c}$ | C. | bac>abc | D. | logac>logbc |
9.已知集合U=R(R是实数集),A={x|-1≤x≤1},B={x|x2-2x<0},则A∪(∁UB)=( )
| A. | [-1,0] | B. | [1,2] | C. | [0,1] | D. | (-∞,1]∪[2,+∞) |
19.(文)已知x,y满足(1+i)+(2-3i)=a+bi,则a,b分别等于( )
| A. | 3,-2 | B. | 3,2 | C. | 3,-3 | D. | -1,4 |
6.在△ABC中,若B=2A,$a:b=1:\sqrt{3}$,则A=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
15.已知等差数列{an}满足a3+a13-a8=2,则{an}的前15项和S15=( )
| A. | 60 | B. | 30 | C. | 15 | D. | 10 |
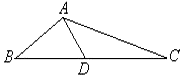 如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$
如图所示,在△ABC中,AB=3$\sqrt{6},B=\frac{π}{4}$,D是BC边上一点,且∠ADB=$\frac{π}{3}$