题目内容
14.已知△ABC的外接圆O的半径为5,AB=6,若$\overrightarrow{CH}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,则|$\overrightarrow{OH}$|的最小值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 作出向量示意图,利用垂径定理得出CH的长,从而得出OH的最小值.
解答 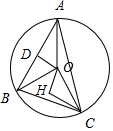 解:设AB中点为D,连结OD,则OD⊥AB,AD=$\frac{1}{2}$AB=3,OA=5,
解:设AB中点为D,连结OD,则OD⊥AB,AD=$\frac{1}{2}$AB=3,OA=5,
∴OD=$\sqrt{O{A}^{2}-A{D}^{2}}$=4,$\overrightarrow{OD}$=$\frac{1}{2}$($\overrightarrow{OA}+\overrightarrow{OB}$),
∴CH=|$\overrightarrow{CH}$|=|$\overrightarrow{OA}+\overrightarrow{OB}$|=2OD=8,
又OC=5,
当O,C,H三点共线时,OH取得最小值CH-OC=3.
故选A.
点评 本题考查了平面向量在几何中的应用,属于中档题.

练习册系列答案
相关题目
4.在中学生综合素质评价某个维度的测评中,分“优秀”“合格”“尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并做出频数统计表如下:
表一:男生的测评结果
表二:女生的测评结果
(1)根据题意求表一和表二中的x和y的值;并由表中统计数据写下面的2×2列联表;
(2)根据所填的列联表判断是否有95%的把握认为“测评结果是否优秀与性别有关”.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
表一:男生的测评结果
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5.已知函数f(x)=6-x3,g(x)=ex-1,则这两个函数的导函数分别为( )
| A. | f′(x)=6-3x2,g′(x)=ex | B. | f′(x)=-3x2,g′(x)=ex-1 | ||
| C. | f′(x)=-3x2,g′(x)=ex | D. | f′(x)=6-3x2,g′(x)=ex-1 |
9.设复数z满足z(1+i)=4,则|$\overline{z}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 8 | C. | 2-2i | D. | 2+2i |