题目内容
4.在中学生综合素质评价某个维度的测评中,分“优秀”“合格”“尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并做出频数统计表如下:表一:男生的测评结果
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)根据分层抽样原理知男生、女生抽取的人数,计算x、y的值;由表中统计数据填写列联表;
(2)计算观测值,对照临界值得出结论.
解答 解:(1)根据题意知,男生应抽取45×$\frac{500}{900}$=25人,
∴x=25-15-5=5;
女生应抽取45-25=20人,
∴y=20115-3=2;
由表中统计数据写2×2列联表如下;
| 男生 | 女生 | 合计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | 10 | 5 | 15 |
| 合计 | 25 | 20 | 45 |
∴没有95%的把握认为“测评结果是否优秀与性别有关”.
点评 本题考查了分层抽样方法与独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
7.已知函数f(x)是定义域为R的奇函数,且当x≥0时,f(x)=log2(x+1)+2x-a,则满足f(x2-3x-1)+9<0的实数x的取值范围是( )
| A. | (-2,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,2) |
15.设a=log85,b=log43,c=($\frac{4}{5}$)2,则a,b,c的大小关系是( )
| A. | b>a>c | B. | a>b>c | C. | c>a>b | D. | a>c>b |
19.有下列一列数:1,8,27,64, ,216,343,…,按照此规律,横线中的数应为( )
| A. | 75 | B. | 100 | C. | 125 | D. | 150 |
9.某学校高三年级有学生500人,其中男生300名,女生200名,为了研究学生的数学成绩(单位:分)是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学成绩,然后按性别分为男、女两组,再将两组学生的数学成绩分成5组,分别加以统计,得到如图所示的频率分布直方图.
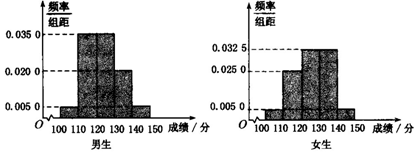
(1)从样本中数学成线小于110分的学生中随机抽取2名学生,求2名学生恰好为一男一女的概率;
(2)若规定数学成绩不小于130分的学生为“数学尖子生”,得到如下数据表:请你根据已知条件完成下列2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.

(1)从样本中数学成线小于110分的学生中随机抽取2名学生,求2名学生恰好为一男一女的概率;
(2)若规定数学成绩不小于130分的学生为“数学尖子生”,得到如下数据表:请你根据已知条件完成下列2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
| 数学尖子生 | 数学尖子生 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 | 100 |
| P(K2≥k2) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |