题目内容

4．已知$\overrightarrow a=（2，1）$，$\overrightarrow b=（m，-1）$，且$\overrightarrow a⊥（\overrightarrow a-\overrightarrow b）$，则实数m=（　　）
A．1B．2C．3D．4

分析 $\overrightarrow a⊥（\overrightarrow a-\overrightarrow b）$，可得$\overrightarrow{a}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）=0，解得m．

解答 解：$\overrightarrow{a}$-$\overrightarrow{b}$=（2-m，2）．
∵$\overrightarrow a⊥（\overrightarrow a-\overrightarrow b）$，∴$\overrightarrow{a}$•（$\overrightarrow{a}$-$\overrightarrow{b}$）=2（2-m）+2=0，解得m=3．
故选：C．

点评 本题考查了向量垂直与数量积的关系，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
14．已知△ABC的外接圆O的半径为5，AB=6，若$\overrightarrow{CH}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$，则|$\overrightarrow{OH}$|的最小值是（　　）
A．3B．4C．5D．6
15．设f（x）是定义在R上的函数，它的图象关于点（1，0）对称，当x≤1时，f（x）=2xe-x（e为自然对数的底数），则f（2+3ln2）的值为（　　）
A．48ln2B．40ln2C．32ln2D．24ln2
12．已知x，y满足约束条件$\left\{\begin{array}{l}{x-2≥0}\\{x+y≤6}\\{2x-y≤6}\end{array}\right.$则目标函数z=$\frac{2y}{x+2}$的最大值为2．
19．若单位向量$\overrightarrow{e_1}，\overrightarrow{e_2}$的夹角为$\frac{π}{3}$，则向量$\overrightarrow{e_1}-2\overrightarrow{e_2}$与向量$\overrightarrow{e_1}$的夹角为$\frac{π}{2}$．
9．等比数列{an}的前n项和Sn=$\frac{1}{2}•{3^{n+1}}$+c（c为常数），若λan≤3+S2n恒成立，则实数λ的最大值是（　　）
A．3B．4C．5D．6
16．双曲线W：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）一个焦点为F（2，0），若点F到W的渐近线的距离是1，则W的离心率为（　　）
A．$\frac{4}{3}$B．$\frac{2\sqrt{3}}{3}$C．2D．$\frac{1}{2}$
13．“=”在基本算法语句中叫（　　）
A．赋值号B．等号C．输入语句D．输出语句
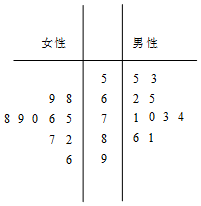14．某城市为了满足市民出行的需要和节能环保的要求，在公共场所提供单车共享服务，某部门为了对该城市共享单车进行监管，随机选取了20位市民对共享单车的情况进行问卷调查，并根据其满意度评分值（满分100分）制作的茎叶图如图所示：
（1）分别计算男性打分的平均数和女性打分的中位数；
（2）从打分在70分以下（不含70分）的市民中抽取3人，求有女性被抽中的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网