题目内容
已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x2+6x+5．（Ⅰ）求函数f（x）的解析式并画出其图象；
（Ⅱ）根据函数f（x）的图象，写出函数f（x）的单调递增区间及值域．
考点：函数图象的作法,函数解析式的求解及常用方法
专题：函数的性质及应用
分析：首先画出当x≤0时，f（x）=x2+6x+5的图象，然后利用偶函数的图象关于y轴对称，得到x＜0的图象，根据图象写出单调区间和最值．
解答：
解：（Ⅰ）当x≤0时，f（x）=x2+6x+5，
∴x＞0时，-x＜0，f（-x）=（-x）2-6x+5=x2-6x+5．
所以函数f（x）的解析式为f(x)=
，
图象如下：
（Ⅱ）由图象可知，函数f（x）的递增区间为[-3，0]，[3，+∞），值域为[-4，+∞）
∴x＞0时，-x＜0，f（-x）=（-x）2-6x+5=x2-6x+5．
所以函数f（x）的解析式为f(x)=
|
图象如下：
（Ⅱ）由图象可知，函数f（x）的递增区间为[-3，0]，[3，+∞），值域为[-4，+∞）
点评：本题考查了函数图象的做法以及由图象得到函数的单调区间和值域．
练习册系列答案
相关题目
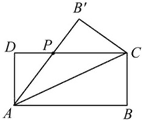设矩形ABCD（AB＞AD）的周长为24，把它关于AC折起来，AB折过去后交CD于点P，如图，设AB=x，求△ADP的面积的最大值，及此时x的值．