题目内容
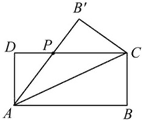 设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.
设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后交CD于点P,如图,设AB=x,求△ADP的面积的最大值,及此时x的值.考点:函数解析式的求解及常用方法
专题:不等式的解法及应用
分析:设AB=x,则AD=12-x,利用勾股定理得打PD,再根据三角形的面积公式个基本不等式的性质,即可求出.
解答:
解∵设AB=x,则AD=12-x,又DP=PB′,AP=AB′-PB′=AB-DP,即AP=x-DP,
∴(12-x)2+PD2=(x-PD)2,得PD=12-
,
∵AB>AD,
∴6<x<12,
∴△ADP的面积S=
AD•DP=
(12-x)(12-
)=108-6(x+
)≤108-6•2
=108-72
,当且仅当x=
即x=6
时取等号,
∴△ADP面积的最大值为108-72
,此时x=6
.
∴(12-x)2+PD2=(x-PD)2,得PD=12-
| 72 |
| x |
∵AB>AD,
∴6<x<12,
∴△ADP的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 72 |
| x |
| 72 |
| x |
| 72 |
| 2 |
| 72 |
| x |
| 2 |
∴△ADP面积的最大值为108-72
| 2 |
| 2 |
点评:本题主要考查了三角形面积公式和基本不等式的性质,属于基础题.

练习册系列答案
相关题目
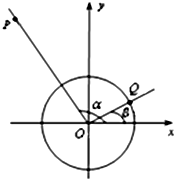 如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为
如图所示,已知α的终边所在直线上的一点P的坐标为(-3,4),β的终边在第一象限且与单位圆的交点Q的纵坐标为 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+6x+5.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+6x+5.