题目内容
把下列方程化为直角坐标方程(并说明对应的曲线):
①ρ=-4cosθ+2sinθ;
②
(θ为参数).
①ρ=-4cosθ+2sinθ;
②
|
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:坐标系和参数方程
分析:①首先,等式两边同乘以ρ,然后,再结合互化公式进行求解;
②首先,将给定的参数方程,对第一个方程平方,然后和第二个方程相加,消去参数即可.
②首先,将给定的参数方程,对第一个方程平方,然后和第二个方程相加,消去参数即可.
解答:
解:①∵ρ=-4cosθ+2sinθ,
两边同乘以ρ,得
ρ2=-4ρcosθ+2ρsinθ,
∴x2+y2=-4x+2y,
∴x2+y2+4x-2y=0
∴(x+2)2+(y-1)2=5,
它表示一个以(-2,1)为圆心,以
为半径的圆.
②∵
(θ为参数).
将x=sinθ两边平方,得
x2=sin2θ,
两式相加,得
y=-x2-6(-1≤x≤1),
它表示的曲线为抛物线的一部分.
两边同乘以ρ,得
ρ2=-4ρcosθ+2ρsinθ,
∴x2+y2=-4x+2y,
∴x2+y2+4x-2y=0
∴(x+2)2+(y-1)2=5,
它表示一个以(-2,1)为圆心,以
| 5 |
②∵
|
将x=sinθ两边平方,得
x2=sin2θ,
两式相加,得
y=-x2-6(-1≤x≤1),
它表示的曲线为抛物线的一部分.
点评:本题重点考查了极坐标方程和普通方程的互化,参数方程和普通方程的互化等知识,属于中档题.

练习册系列答案
相关题目
 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+6x+5.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+6x+5.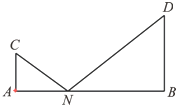 如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.
如图,C,D是两个小区的所在地,C,D到一条公路AB的垂直距离CA=1km,DB=2km,AB两端之间的距离为4km.某公交公司将在AB之间找一点N,在N处建造一个公交站台.