题目内容
已知-1≤x≤0,求函数y=2x+1-3•4x的最大值和最小值.
考点:函数的最值及其几何意义
专题:计算题
分析:现将函数y=2x+1-3•4x变形、转化为二次函数.进而根据已知可求出最大值和最小值.
解答:
(本题12分)
解:令y=2x+1-3•4x=-3•(2x)2+2•2x
令t=2x则y=-3t2+2t=-3(t-
)2+
,…-1≤x≤0,∴
≤2x≤1即t∈[
,1]
又∵对称轴t=
∈[
,1],∴当t=
,即x=log2
时ymax=
.
∴当 t=1即x=0时,ymin=
.
解:令y=2x+1-3•4x=-3•(2x)2+2•2x
令t=2x则y=-3t2+2t=-3(t-
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
又∵对称轴t=
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴当 t=1即x=0时,ymin=
| 1 |
| 3 |
点评:本题考查了函数的最值及其几何意义,属于基础题.

练习册系列答案
相关题目
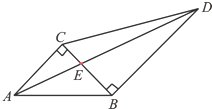 如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°.
如图,两块直角三角板拼在一起,已知∠ABC=45°,∠BCD=60°. 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+6x+5.
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+6x+5.