题目内容
已知抛掷一枚质地均匀的硬币,正面朝上的概率为0.5,现采用随机模拟试验的方法估计抛掷这枚硬币三次恰有两次正面朝上的概率;先由计算器产生0或1的随机数,用0表示正面朝上,用1表示反面朝上;再以每三个随机数做为一组,代表这三次投掷的结果,经随机模拟试验产生了如下20组随机数:
101 111 010 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率为( )
101 111 010 101 010 100 100 011 111 110
000 011 010 001 111 011 100 000 101 101
据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率为( )
| A、0.30 | B、0.35 |
| C、0.40 | D、0.65 |
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:总得事件共有20种,恰有两次正面朝上有010,010,100,100,010,001,100,共7种,根据概率公式计算即可
解答:
解:总得事件共有20种,恰有两次正面朝上有010,010,100,100,010,001,100,共7种,
故据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率P=
=0.35,
故选:B
故据此估计,抛掷这枚硬币三次恰有两次正面朝上的概率P=
| 7 |
| 20 |
故选:B
点评:本题考查了古典概型概率的问题,属于基础题

练习册系列答案
相关题目
 一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )
一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是2的圆,则这个几何体的表面积是( )| A、16π | B、14π |
| C、12π | D、8π |
双曲线C:
-
=1(a>0,b>0)的左右焦点分别为F1、F2,离心率为
,过F1且与x轴垂直的直线与双曲线C交于A,B两点,则|AF1|与|AF2|的关系是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2|AF2|=3|AF1| |
| B、|AF2|=2|AF1| |
| C、|AF2|=3|AF1| |
| D、3|AF2|=4|AF1| |
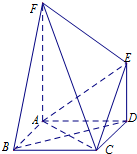 如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.
如图所示的几何体中,直线AF⊥平面ABCD,且ABCD为正方形,ADEF为梯形,DE∥AF,又AB=1,AF=2DE=2a.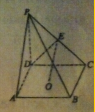
 如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.
如图,A、B两点都在河的对岸(不可到达),某人想测量A、B之间的距离,但只有卷尺和测角仪两种工具,若此人在地面上选一条基线EF,用卷尺测得EF的长度为a,且用测角仪测量了一些角度:∠AEB=α,∠AEF=β,∠BFE=γ,∠AFB=δ.请你用文字和公式写出计算A、B之间距离的步骤.


