题目内容
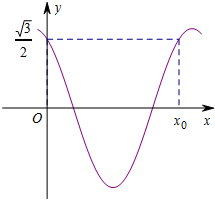 函数f(x)=cos(πx+φ)(0<φ<
函数f(x)=cos(πx+φ)(0<φ<| π |
| 2 |
(Ⅰ)写出φ及图中x0的值;
(Ⅱ)设g(x)=f(x)+f(x+
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
考点:余弦函数的图象
专题:三角函数的求值,三角函数的图像与性质
分析:(Ⅰ)由题意可得
=cos(0+φ),可得φ的值.由
=cos(πx0+
),可得x0的值.
(Ⅱ)先求得g(x)的函数解析式,由 x∈[-
,
],可得-
≤πx+
≤
,从而可求函数g(x)在区间[-
,
]上的最大值和最小值.
| ||
| 2 |
| ||
| 2 |
| π |
| 6 |
(Ⅱ)先求得g(x)的函数解析式,由 x∈[-
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答:
(共13分)
解:(Ⅰ)∵
=cos(0+φ)
∴φ的值是
.…(2分)
∵
=cos(πx0+
)
∴2π-
=πx0+
,可得x0的值是
.…(5分)
(Ⅱ)由题意可得:f(x+
)=cos(π(x+
)+
)=cos(πx+
)=-sinπx.…(7分)
所以 f(x)+f(x+
)=cos(πx+
)-sinπx=cosπxcos
-sinπxsin
-sinπx…(8分)
=
cosπx-
sinπx-sinπx=
cosπx-
sinπx=
cos(πx+
).…(10分)
因为 x∈[-
,
],
所以 -
≤πx+
≤
.
所以 当πx+
=0,即x=-
时,g(x)取得最大值
;
当πx+
=
,即x=
时,g(x)取得最小值-
.…(13分)
解:(Ⅰ)∵
| ||
| 2 |
∴φ的值是
| π |
| 6 |
∵
| ||
| 2 |
| π |
| 6 |
∴2π-
| π |
| 6 |
| π |
| 6 |
| 5 |
| 3 |
(Ⅱ)由题意可得:f(x+
| 1 |
| 3 |
| 1 |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以 f(x)+f(x+
| 1 |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
=
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 3 |
因为 x∈[-
| 1 |
| 2 |
| 1 |
| 3 |
所以 -
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
所以 当πx+
| π |
| 3 |
| 1 |
| 3 |
| 3 |
当πx+
| π |
| 3 |
| 2π |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
点评:本题主要考察了,三角函数化简求值,三角函数的图象与性质,三角函数最值的解法,属于中档题.

练习册系列答案
相关题目
双曲线C:
-
=1(a>0,b>0)的左右焦点分别为F1、F2,离心率为
,过F1且与x轴垂直的直线与双曲线C交于A,B两点,则|AF1|与|AF2|的关系是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| A、2|AF2|=3|AF1| |
| B、|AF2|=2|AF1| |
| C、|AF2|=3|AF1| |
| D、3|AF2|=4|AF1| |
椭圆
+
=1上的一点P到椭圆一个焦点的距离为5,则点P到另一个焦点的距离为( )
| x2 |
| 36 |
| y2 |
| 9 |
| A、7 | B、5 | C、4 | D、1 |
函数y=
log2|x|的大致图象是( )
| x |
| |x| |
A、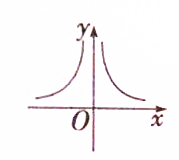 |
B、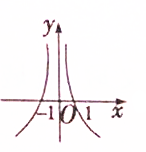 |
C、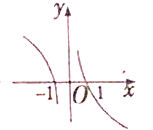 |
D、 |
