题目内容
 已知y=f(x)是定义在R上的奇函数,且x>0时,f(x)=1+(
已知y=f(x)是定义在R上的奇函数,且x>0时,f(x)=1+(| 1 |
| 2 |
(1)求函数f(x)的解析式;
(2)画出函数f(x)的草图;
(3)利用图象直接写出函数f(x)的单调区间及值域.
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:(1)根据f(x)是定义在R上的奇函数得f(0)=0,当x<0时则-x<0,由f(x)=-f(-x)求出x<0时的解析式,再用分段函数的形式表示出f(x);
(2)根据解析式和指数函数的图象,画出该函数的草图;
(3)根据函数的图象求出f(x)的单调区间及值域.
(2)根据解析式和指数函数的图象,画出该函数的草图;
(3)根据函数的图象求出f(x)的单调区间及值域.
解答:
解:(1)由题意得,当x=0时,f(0)=0,…(2分)
当x<0时,则-x<0,f(x)=-f(-x)=-(1+(
)-x)=-1-2-x,
故f(x)的解析式为:f(x)=
…(6分)
(2)函数草图如右;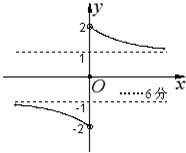 …(10分)
…(10分)
(3)由图得,减区间为(-∞,0),(0,+∞);值域为{y|-2<y<-1或y=0或1<y<2} …(12分)
当x<0时,则-x<0,f(x)=-f(-x)=-(1+(
| 1 |
| 2 |
故f(x)的解析式为:f(x)=
|
(2)函数草图如右;
 …(10分)
…(10分)(3)由图得,减区间为(-∞,0),(0,+∞);值域为{y|-2<y<-1或y=0或1<y<2} …(12分)
点评:本题考查函数的奇偶性和单调性的应用,指数函数的图象和图象的平移变换,考查了作图和识图能力.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
用二分法求方程3x+3x-8=0在(1,2)内近似解的过程中,设f(x)=3x+3x-8,得f(1)<0,f(1.5)>0,f(1.25)>0,则该方程的根落在区间( )
| A、(1,1.25) |
| B、(1.25,1.5) |
| C、(1.5,2) |
| D、不能确定 |
x0是函数y=x3-(
)x的零点,则x0所在的区间是( )
| 1 |
| 2 |
| A、(3,4) |
| B、(2,3) |
| C、(1,2) |
| D、(0,1) |
设曲线y=|3-x2|和直线y=a(a∈R)的公共点的个数为m,则下列四种情况不可能的是( )
| A、m=1 | B、m=2 |
| C、m=3 | D、m=4 |
连掷两次骰子得到的点数分别为m和n,则向量
=(m,n)与向量
=(1,-1)数量积大于0的概率为( )
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|