题目内容
设曲线y=|3-x2|和直线y=a（a∈R）的公共点的个数为m，则下列四种情况不可能的是（ ）
| A、m=1 | B、m=2 |
| C、m=3 | D、m=4 |
考点：二次函数的图象
专题：函数的性质及应用
分析：根据二次函数的图象函数，利用数形结合即可得到结论．
解答：
解：∵y=|3-x2|=y=|x2-3|为偶函数，
∴函数关于y轴对称，
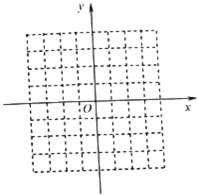
作出函数的图象如图：
当a＜0时，公共点的个数m=0，
当a=0时，公共点的个数m=2，
当0＜a＜3时，公共点的个数m4，
当a=3时，公共点的个数m=3，
当a＞3时，公共点的个数m=2，
故不可能是A，
故选：A
∴函数关于y轴对称，
作出函数的图象如图：
当a＜0时，公共点的个数m=0，
当a=0时，公共点的个数m=2，
当0＜a＜3时，公共点的个数m4，
当a=3时，公共点的个数m=3，
当a＞3时，公共点的个数m=2，
故不可能是A，
故选：A
点评：本题主要考查二次函数的图象和性质，作出函数的图象利用数形结合是解决本题的关键．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
设F1和F2是椭圆
+y2=1的两个焦点，点P在双曲线上，且满足∠F1PF2=90°，则△PF1F2的面积是（ ）
| x2 |
| 4 |
A、
| ||||
| B、1 | ||||
| C、2 | ||||
D、
|
已知点A的直角坐标为（
，-
），则它的极坐标为（ ）
| 1 |
| 2 |
| 1 |
| 2 |
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|
已知y=f（x）是定义在R上的奇函数，且x＞0时，f（x）=1+（要得到函数y=sinx+cosx的图象，只需将曲线y=
sinx上所有的点（ ）
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
不等式
≤0的解集为（ ）
| 3x-1 |
| x-2 |
A、{x|
| ||
B、{x|
| ||
C、{x|x＞2或x≤
| ||
| D、{x|x＜2} |
已知过点A（-2，m）和B（m，4）的直线l：与直线2x+y-1=0垂直，则l的方程是（ ）
| A、x-2y+6=0 |
| B、.x-y-6=0 |
| C、x-2y-6=0 |
| D、x-y+6=0 |