题目内容
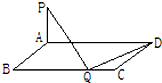 已知在矩形ABCD中,AB=2
已知在矩形ABCD中,AB=2| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|
考点:直线与平面垂直的判定
专题:计算题,空间位置关系与距离
分析:PA⊥平面ABCD,PQ⊥QD可得QD⊥AQ,可得△ABQ∽△QCD,可求a的范围,即可求出a的最小值.
解答:
解:假设在BC边上存在点Q,使得PQ⊥QD,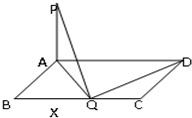
因为PA⊥平面ABCD,所以PA⊥QD,又由于PQ⊥QD,
所以QD⊥平面APQ,则QD⊥AQ,即∠AQD=90°,
易得△ABQ∽△QCD,设BQ=x,所以有x(a-x)=8
即:x2-ax+8=0
所以当△=a2-32≥0时,上方程有解,
因此,当a≥4
时,存在符合条件的点Q,
所以a的最小值是4
.
故选:D.

因为PA⊥平面ABCD,所以PA⊥QD,又由于PQ⊥QD,
所以QD⊥平面APQ,则QD⊥AQ,即∠AQD=90°,
易得△ABQ∽△QCD,设BQ=x,所以有x(a-x)=8
即:x2-ax+8=0
所以当△=a2-32≥0时,上方程有解,
因此,当a≥4
| 2 |
所以a的最小值是4
| 2 |
故选:D.
点评:本题主要考查了直线与平面垂直的性质,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
已知函数f(3x+1)=x2+3x+2,则f(4)=( )
| A、30 | B、6 | C、210 | D、9 |
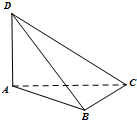 如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=
如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=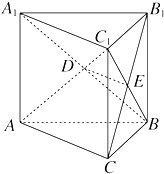 如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.
如图所示,直三棱柱ABC-A1B1C1的侧棱长和底面边长都是a,截面AB1C和截面A1BC1相交于DE,求四面体B-B1DE的体积.