题目内容
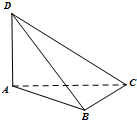 如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=
如图,在四面体ABCD中,已知DA⊥面ABC,BC⊥面ABD,BC=BD=2,四面体的三个面DAB、DBC、DCA面积的平方和是8,则∠ADB=考点:直线与平面垂直的性质
专题:计算题,空间位置关系与距离
分析:先证明DA⊥AB,DA⊥AC,BC⊥BD,BC⊥AB,再设AD=a,AB=b,则a2+b2=4,利用三个面DAB、DBC、DCA面积的平方和是8,BC=BD=2,建立方程,求出a,b,即可求出∠ADB.
解答:
解:∵DA⊥面ABC,
∴DA⊥AB,DA⊥AC,
∵BC⊥面ABD,
∴BC⊥BD,BC⊥AB,
设AD=a,AB=b,则a2+b2=4,
∵三个面DAB、DBC、DCA面积的平方和是8,BC=BD=2,
∴(
ab)2+(
×2×2)2+(
×a×
)2=8,
∴a=b=
,
∴∠ADB=45°,
故答案为:45°.
∴DA⊥AB,DA⊥AC,
∵BC⊥面ABD,
∴BC⊥BD,BC⊥AB,
设AD=a,AB=b,则a2+b2=4,
∵三个面DAB、DBC、DCA面积的平方和是8,BC=BD=2,
∴(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| b2+4 |
∴a=b=
| 2 |
∴∠ADB=45°,
故答案为:45°.
点评:本题考查直线与平面垂直的性质,考查学生的计算能力,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知集合A={x||x|<3},集合B={x|x-2≥0},则A∪(∁RB)等于( )
| A、(-∞,3] |
| B、(-∞,3) |
| C、[2,3) |
| D、(-3,2] |
 如图,甲烷CH4 的分子结构是:碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上.设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则cosθ=( )
如图,甲烷CH4 的分子结构是:碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上.设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则cosθ=( )| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
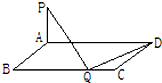 已知在矩形ABCD中,AB=2
已知在矩形ABCD中,AB=2| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|