题目内容
设函数f(x)=x2-x+alnx,其中a≠0.
(1)若a=-6,求f(x)在[1,4]上的最值;
(2)若f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(3)求证:不等式ln
>
(n∈N*)恒成立.
(1)若a=-6,求f(x)在[1,4]上的最值;
(2)若f(x)在定义域内既有极大值又有极小值,求实数a的取值范围;
(3)求证:不等式ln
| n+1 |
| n |
| n-1 |
| n3 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)当a=-6时,由f′(x)=0得x=2,可判断出当x∈[1,2)时,f(x)单调递减;当x∈(2,4]时,
f(x)单调递增,从而得到f(x)在[1,4]上的最值.
(2)要使f(x)在定义域内既有极大值又有极小值,即f(x)在定义域内与X轴有三个不同的交点,即使f′(x)=0在(0,+∞)有两个不等实根,即2x2-x+a=0在(0,+∞)有两不等实根,可以利用一元二次函数根的分布,即可求a的范围.
(3)先构造函数h(x)=x3-x2+ln(x+1),然后研究h(x)在[0,+∞)上的单调性,求出函数h(x)的最小值,从而得到ln(x+1)>x2-x3,最后令x=
,即可证得结论.
f(x)单调递增,从而得到f(x)在[1,4]上的最值.
(2)要使f(x)在定义域内既有极大值又有极小值,即f(x)在定义域内与X轴有三个不同的交点,即使f′(x)=0在(0,+∞)有两个不等实根,即2x2-x+a=0在(0,+∞)有两不等实根,可以利用一元二次函数根的分布,即可求a的范围.
(3)先构造函数h(x)=x3-x2+ln(x+1),然后研究h(x)在[0,+∞)上的单调性,求出函数h(x)的最小值,从而得到ln(x+1)>x2-x3,最后令x=
| 1 |
| n |
解答:
解:(1)当a=-6时,f(x)=x2-x-6lnx(x>0),
f′(x)=2x-1-
=
=
,
令f′(x)=0⇒x1=2,x2=-
(舍),
当1≤x<2时,f′(x)0.
∴f(x)在[1,2]上为减函数,在[2,4]上为增函数.
∴f(x)min=f(2)=2-6ln2,f(1)=0,f(4)=12-6ln4>0.
∴f(x)max=f(4)=12-6ln4=12(1-ln2);
(2)f(x)在定义域内既有极大值又有极小值,
即f′(x)=0在(0,+∞)有两不等根,
即2x2-x+a=0在(0,+∞)有两不等实根,
令g(x)=2x2-x+a,则
,解得0<a<
;
(3)令函数h(x)=x3-f(x)=x3-x2+ln(x+1)
则h′(x)=3x2-2x+
=
,
∴当x∈[0,+∞)时,h′(x)>0
∴函数h(x)在[0,+∞)上单调递增,
又h(0)=0,
∴x∈(0,+∞)时,恒有h(x)>h(0)=0
即x2<x3+ln(x+1)恒成立.
取x=
∈(0,+∞),则有ln(
+1)>
-
恒成立.
即不等式ln
>
(n∈N*)恒成立.
f′(x)=2x-1-
| 6 |
| x |
| 2x2-x-6 |
| x |
| (x-2)(2x+3) |
| x |
令f′(x)=0⇒x1=2,x2=-
| 3 |
| 2 |
当1≤x<2时,f′(x)0.
∴f(x)在[1,2]上为减函数,在[2,4]上为增函数.
∴f(x)min=f(2)=2-6ln2,f(1)=0,f(4)=12-6ln4>0.
∴f(x)max=f(4)=12-6ln4=12(1-ln2);
(2)f(x)在定义域内既有极大值又有极小值,
即f′(x)=0在(0,+∞)有两不等根,
即2x2-x+a=0在(0,+∞)有两不等实根,
令g(x)=2x2-x+a,则
|
| 1 |
| 8 |
(3)令函数h(x)=x3-f(x)=x3-x2+ln(x+1)
则h′(x)=3x2-2x+
| 1 |
| x+1 |
| 3x3+(x-1)2 |
| x+1 |
∴当x∈[0,+∞)时,h′(x)>0
∴函数h(x)在[0,+∞)上单调递增,
又h(0)=0,
∴x∈(0,+∞)时,恒有h(x)>h(0)=0
即x2<x3+ln(x+1)恒成立.
取x=
| 1 |
| n |
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n3 |
即不等式ln
| n+1 |
| n |
| n-1 |
| n3 |
点评:本题以函数为载体,考查函数的最值,考查函数的单调性.第一问判断f(x)在定义域的单调性即可求出最小值.第二问将f(x)在定义域内既有极大值又有极小值问题转化为f(x)在定义域内与X轴有三个不同的交点是解题的关键,第三问的关键是构造新函数,利用导数证明不等式,是压轴题.

练习册系列答案
相关题目
 如图,甲烷CH4 的分子结构是:碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上.设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则cosθ=( )
如图,甲烷CH4 的分子结构是:碳原子位于正四面体的中心,4个氢原子分别位于正四面体的四个顶点上.设碳原子与4个氢原子连成的四条线段两两组成的角为θ,则cosθ=( )| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
设函数f(x)=x2+bln(x+1),其中b≠0.
(1)如果函数f(x)在定义域内既有极大值又有极小值,求实数b的取值范围;
(2)求证对任意的n∈N*,不等式ln(
+1)>
-
都成立.
(1)如果函数f(x)在定义域内既有极大值又有极小值,求实数b的取值范围;
(2)求证对任意的n∈N*,不等式ln(
| 1 |
| n |
| 1 |
| n2 |
| 1 |
| n3 |
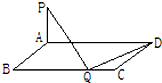 已知在矩形ABCD中,AB=2
已知在矩形ABCD中,AB=2| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|