题目内容
已知函数f（x）=sin（2x-
），x∈R．
（1）求f（
）的值；
（2）求该函数取得最大值时自变量的取值集合；
（3）设α是第三象限角，且f（α+
）=
，求sinα的值．
| π |
| 6 |
（1）求f（
| π |
| 4 |
（2）求该函数取得最大值时自变量的取值集合；
（3）设α是第三象限角，且f（α+
| π |
| 3 |
| 3 |
| 5 |
考点：正弦函数的图象
专题：三角函数的求值
分析：（1）由函数f（x）的解析式求得f（
）的值．
（2）根据正弦函数的值域求得该函数取得最大值时自变量的取值集合．
（3）由α是第三象限角以及f（α+
）=
，利用二倍角的余弦公式求得sinα的值．
| π |
| 4 |
（2）根据正弦函数的值域求得该函数取得最大值时自变量的取值集合．
（3）由α是第三象限角以及f（α+
| π |
| 3 |
| 3 |
| 5 |
解答：
解：（1）∵函数f（x）=sin（2x-
），∴f（
）=sin
=
．
（2）当且仅当2x-
=2kπ+
，k∈z时，即x=kπ+
时，该函数取得最大值1，
所以该函数取得最大值时自变量的取值集合为{x|x=kπ+
，k∈z}．
（3）由f（α+
）=
，求得cos2α=
=1-2sin2α，∴sinα=±
．
再结合α是第三象限角，可得sinα=-
．
| π |
| 6 |
| π |
| 4 |
| π |
| 3 |
| ||
| 2 |
（2）当且仅当2x-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
所以该函数取得最大值时自变量的取值集合为{x|x=kπ+
| π |
| 3 |
（3）由f（α+
| π |
| 3 |
| 3 |
| 5 |
| 3 |
| 5 |
| ||
| 5 |
再结合α是第三象限角，可得sinα=-
| ||
| 5 |
点评：本题主要考查正弦函数的定义域和值域，同角三角函数的基本关系，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
已知集合A={x||x|＜3}，集合B={x|x-2≥0}，则A∪（∁RB）等于（ ）
| A、（-∞，3] |
| B、（-∞，3） |
| C、[2，3） |
| D、（-3，2] |
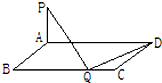已知在矩形ABCD中，AB=2| 2 |
| A、1 | ||
B、
| ||
C、2
| ||
D、4
|