题目内容
2.函数y=log2(3cosx+1),x∈[-$\frac{π}{2}$,$\frac{π}{2}$]的值域为[0,2].分析 根据x∈[-$\frac{π}{2}$,$\frac{π}{2}$],得出1≤3cosx+1≤4,利用对数函数的性质,即可得出结论.
解答 解:∵x∈[-$\frac{π}{2}$,$\frac{π}{2}$],∴0≤cosx≤1,
∴1≤3cosx+1≤4,
∴0≤log2(3cosx+1)≤2,
故答案为[0,2].
点评 本题考查三角函数、对数函数的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
12.在△ABC中,a,b,c分别是A,B,C的对边,$a=2\sqrt{3},b=2\sqrt{2}$,且1+2cos(B+C)=0,则BC边上的高等于( )
| A. | $2({\sqrt{3}+1})$ | B. | $2({\sqrt{3}-1})$ | C. | $\sqrt{3}+1$ | D. | $\sqrt{3}-1$ |
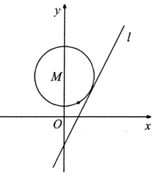 已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).
已知直线l:y=2x+n,n∈R,圆M的圆心在y轴,且过点(1,1).