题目内容
13．已知圆O：x2+y2=16上任意一点P，过P作x轴的垂线段PA，A为垂足，当点P在圆上运动时，线段PA的中点M的轨迹记为曲线C，则曲线C的离心率为$\frac{\sqrt{3}}{2}$．分析 利用已知条件求出椭圆的方程，然后利用椭圆的离心率即可．
解答 解：设M（x，y），则P（x，2y），代入圆的方程并化简得：$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$，
解得a=4，b=2，c=$2\sqrt{3}$．
椭圆的离心率为：$\frac{\sqrt{3}}{2}$．
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题考查轨迹方程的求法，椭圆的简单性质的应用，考查计算能力．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
3．在数列{an}中，若存在非零实数T，使得${a_{n+T}}={a_n}（{N∈{n^*}}）$成立，则称数列{an}是以T为周期的周期数列．若数列{bn}满足bn+1=|bn-bn-1|，且b1=1，b2=a（a≠0），则当数列{bn}的周期最小时，其前2017项的和为（ ）
| A． | 672 | B． | 673 | C． | 3024 | D． | 1345 |
4．直线x-2y-3=0在y轴上的截距是（ ）
| A． | 3 | B． | $\frac{3}{2}$ | C． | -$\frac{3}{2}$ | D． | -3 |
18．某小组共10人，利用假期参加义工活动．已知参加义工活动的次数与相对应的人数的对应关系如表：
现从这10人中随机选出2人作为该组代表在活动总结会上发言．
（Ⅰ）设A为事件“选出的2人参加义工活动次数之和为6”，求事件A发生的概率；
（Ⅱ）设X为选出的2人参加义工活动次数之和，求随机变量X的分布列和数学期望．
| 次数 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 4 | 1 |
（Ⅰ）设A为事件“选出的2人参加义工活动次数之和为6”，求事件A发生的概率；
（Ⅱ）设X为选出的2人参加义工活动次数之和，求随机变量X的分布列和数学期望．
5．
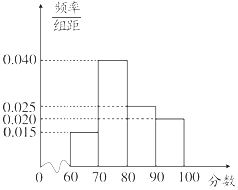2016年年底，某商业集团根据相关评分标准，对所属20家商业连锁店进行了年度考核评估，并依据考核评估得分（最低分60分，最高分100分）将这些连锁店分别评定为A，B，C，D四个类型，其考核评估标准如表：
考核评估后，对各连锁店的评估分数进行统计分析，得其频率分布直方图如下：
（Ⅰ）评分类型为A的商业连锁店有多少家；
（Ⅱ）现从评分类型为A，D的所有商业连锁店中随机抽取两家做分析，求这两家来自同一评分类型的概率．
2016年年底，某商业集团根据相关评分标准，对所属20家商业连锁店进行了年度考核评估，并依据考核评估得分（最低分60分，最高分100分）将这些连锁店分别评定为A，B，C，D四个类型，其考核评估标准如表：| 评估得分 | [60，70） | [70，80） | [80，90） | [90，100] |
| 评分类型 | D | C | B | A |
（Ⅰ）评分类型为A的商业连锁店有多少家；
（Ⅱ）现从评分类型为A，D的所有商业连锁店中随机抽取两家做分析，求这两家来自同一评分类型的概率．
3．已知集合A={-2，0，2}，B={x|x2-x-2=0}，则A∩B=（ ）
| A． | ∅ | B． | {0} | C． | {2} | D． | {-2} |