题目内容
10.已知圆C过点$A(\frac{3}{4},\;0)$,且与直线$l:\;x=-\frac{3}{4}$相切,(I)求圆心C的轨迹方程;
(II) O为原点,圆心C的轨迹上两点M、N(不同于点O)满足$\overrightarrow{OM}•\overrightarrow{ON}=0$,已知$\overrightarrow{OP}=\frac{1}{3}\overrightarrow{OM}$,$\overrightarrow{OQ}=\frac{1}{3}\overrightarrow{ON}$,证明直线PQ过定点,并求出该定点坐标和△APQ面积的最小值.
分析 (I)由已知得圆心C的轨迹是以A为焦点,l为准线的抛物线,即可求圆心C的轨迹方程;
(II) 求出M,N的坐标,可得P,Q的坐标,进而可得直线PQ的方程,从而证明直线PQ过定点,并求出该定点坐标和△APQ面积的最小值.
解答 解:(Ⅰ)由已知得圆心C的轨迹是以A为焦点,l为准线的抛物线,
由$\frac{p}{2}=\frac{3}{4}$得y2=2px=3x,得圆心C的轨迹方程为y2=3x;-------------------------(3分)
(Ⅱ)证明:依题意知OM的斜率k存在,且k≠0,设OM的方程为y=kx,------------(4分)
∵OM⊥ON,则ON的方程为$y=-\frac{1}{k}x$,
由$\left\{{\begin{array}{l}{y=kx}\\{{y^2}=3x}\end{array}}\right.$得k2x2=3x,得${x_M}=\frac{3}{k^2}$,------------------------------------------------------(6分)
同理得${x_N}=3{k^2}$,
由已知得${x_P}=\frac{1}{k^2}$,${x_N}={k^2}$,∴$P(\frac{1}{k^2},\;\frac{1}{k})$,Q(k2,-k),----------------------------(8分)
∴${k_{PQ}}=\frac{{-k-\frac{1}{k}}}{{{k^2}-\frac{1}{k^2}}}=-\frac{k}{{{k^2}-1}}$,直线PQ的方程为y+k=$-\frac{k}{{{k^2}-1}}(x-{k^2})$,
即k(x-1)+(k2-1)y=0,∴直线PQ过定点(1,0),---------------------------------(10分)
设B(1,0),则${S_{△APQ}}=\frac{1}{2}|AB|•|{y_P}-{y_Q}|=\frac{1}{2}×\frac{1}{4}×|\frac{1}{k}+k|$=$\frac{1}{8}(|\frac{1}{k}|+|k|)≥\frac{1}{8}×2=\frac{1}{4}$,
∴△APQ面积的最小值为$\frac{1}{4}$.---------------------------------------------------------------------(12分)
点评 本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查三角形面积的计算,属于中档题.

 中考解读考点精练系列答案
中考解读考点精练系列答案| A. | 25 | B. | 23 | C. | 21 | D. | 20 |
| 次数 | 1 | 2 | 3 | 4 |
| 人数 | 1 | 4 | 4 | 1 |
(Ⅰ)设A为事件“选出的2人参加义工活动次数之和为6”,求事件A发生的概率;
(Ⅱ)设X为选出的2人参加义工活动次数之和,求随机变量X的分布列和数学期望.
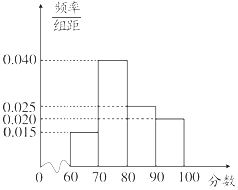 2016年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如表:
2016年年底,某商业集团根据相关评分标准,对所属20家商业连锁店进行了年度考核评估,并依据考核评估得分(最低分60分,最高分100分)将这些连锁店分别评定为A,B,C,D四个类型,其考核评估标准如表:| 评估得分 | [60,70) | [70,80) | [80,90) | [90,100] |
| 评分类型 | D | C | B | A |
(Ⅰ)评分类型为A的商业连锁店有多少家;
(Ⅱ)现从评分类型为A,D的所有商业连锁店中随机抽取两家做分析,求这两家来自同一评分类型的概率.