题目内容
12.在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=4,点D是A1C1的中点,则异面直线AD和BC1所成角的大小为30°.分析 可作出图形,取AC中点E,并连接C1E,BE,从而有C1E∥AD,从而得到∠EC1B或其补角便为异面直线AD和BC1所成角,根据条件可以求出△BC1E的三边长度,从而可以得到∠BEC1=90°,然后求sin∠BC1E,这样即可得出异面直线AD和BC1所成角的大小.
解答 解:如图,取AC中点E,连接C1E,BE,则C1E∥AD;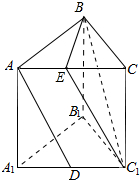
∴∠EC1B或其补角为异面直线AD和BC1所成角;
根据条件得:BE=2$\sqrt{2}$,C1E=2$\sqrt{6}$,BC1=4$\sqrt{2}$;
∴BE2+C1E2=BC12;
∴∠BEC1=90°;
∴sin∠EC1B=$\frac{2\sqrt{2}}{4\sqrt{2}}$=$\frac{1}{2}$;
∴∠EC1B=30°;
∴异面直线AD和BC1所成角的大小为30°.
故答案为:30°
点评 考查异面直线所成角的概念及求法,直角三角形边的关系,正弦函数的定义,以及已知三角函数值求角.

练习册系列答案
相关题目
12.若曲线Cl:x2+y2-2x=0与曲线C2:(x-1)(y-mx-m)=0有四个不同的交点,则实数m的取值范围是( )
| A. | $({-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}})$ | B. | $({-\frac{{\sqrt{3}}}{3},0})∪({0,\frac{{\sqrt{3}}}{3}})$ | C. | $[{-\frac{{\sqrt{3}}}{3},\frac{{\sqrt{3}}}{3}}]$ | D. | $({-∞,-\frac{{\sqrt{3}}}{3}})∪({\frac{{\sqrt{3}}}{3},+∞})$ |
3.在数列{an}中,若存在非零实数T,使得${a_{n+T}}={a_n}({N∈{n^*}})$成立,则称数列{an}是以T为周期的周期数列.若数列{bn}满足bn+1=|bn-bn-1|,且b1=1,b2=a(a≠0),则当数列{bn}的周期最小时,其前2017项的和为( )
| A. | 672 | B. | 673 | C. | 3024 | D. | 1345 |
20.函数f(x)=-x3+3x2+9x+a,x∈[-2,2]的最小值为-2,则f(x)的最大值为( )
| A. | 25 | B. | 23 | C. | 21 | D. | 20 |
17.与双曲线2x2-y2=3有相同渐近线,且过点P(1,2)的双曲线的方程为( )
| A. | 2x2-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{y}^{2}}{2}$-x2=1 | C. | x2-$\frac{{y}^{2}}{2}$=1 | D. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{4}$=1 |
4.直线x-2y-3=0在y轴上的截距是( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | -$\frac{3}{2}$ | D. | -3 |