题目内容
 已知抛物线C的方程为y=
已知抛物线C的方程为y=| 1 |
| 2p |
(1)求抛物线C的方程;
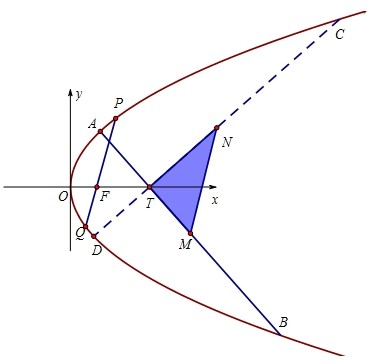
(2)若∠BMN=∠AMN,求证:直线AB的斜率为定值;
(3)若直线AB的斜率为
| 2 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由抛物线C的方程为y=
x2,焦点F(0,1),求出p,即可得到抛物线C的方程;
(2)设A(x1,y1),B(x2,y2),直线AM的斜率为k,由∠BMN=∠AMN,知直线BM的斜率为-k,所以直线AM的方程为y=k(x+2
)-2,由此能够证明直线AB的斜率为定值.
(3)若直线AB的斜率为
,由(2)可得:kAB=
=
=
,知kAM+kBM=0,∠BMN=∠AMN,由点N到直线MA,MB的距离的和为8,知点N到直线MA,MB的距离均为4,由此能得到△MAB是直角三角形.
| 1 |
| 2p |
(2)设A(x1,y1),B(x2,y2),直线AM的斜率为k,由∠BMN=∠AMN,知直线BM的斜率为-k,所以直线AM的方程为y=k(x+2
| 2 |
(3)若直线AB的斜率为
| 2 |
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4 |
| 2 |
解答:
(1)解:∵抛物线C的方程为y=
x2,焦点F(0,1),
∴p=1,
∴抛物线C的方程为x2=4y;
(2)证明:设A(x1,y1),B(x2,y2),直线AM的斜率为k,
∵∠BMN=∠AMN,∴直线BM的斜率为-k,
∵直线y=2交抛物线于M,N两点,
∴M(-2
,2),N(2
,2),
∴直线AM的方程为y=k(x+2
)-2,
代入x2=4y得x2-4kx-8
k-8=0,
∴xMx1=-8
k-8,
∴x1=4k+2
,
同理x2=-4k+2
,
∴kAB=
=
=
.
(3)解:若直线AB的斜率为
,由(2)可得:kAB=
=
=
,
∴kAM+kBM=0,
∴∠BMN=∠AMN,
又点N到直线MA,MB的距离的和为8,
∴点N到直线MA,MB的距离均为4,
∵MN=4
,
∴∠BMN=∠AMN=45°,
∴△MAB是直角三角形.
| 1 |
| 2p |
∴p=1,
∴抛物线C的方程为x2=4y;
(2)证明:设A(x1,y1),B(x2,y2),直线AM的斜率为k,
∵∠BMN=∠AMN,∴直线BM的斜率为-k,
∵直线y=2交抛物线于M,N两点,
∴M(-2
| 2 |
| 2 |
∴直线AM的方程为y=k(x+2
| 2 |
代入x2=4y得x2-4kx-8
| 2 |
∴xMx1=-8
| 2 |
∴x1=4k+2
| 2 |
同理x2=-4k+2
| 2 |
∴kAB=
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4 |
| 2 |
(3)解:若直线AB的斜率为
| 2 |
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4 |
| 2 |
∴kAM+kBM=0,
∴∠BMN=∠AMN,
又点N到直线MA,MB的距离的和为8,
∴点N到直线MA,MB的距离均为4,
∵MN=4
| 2 |
∴∠BMN=∠AMN=45°,
∴△MAB是直角三角形.
点评:本题考查抛物线方程,考查直线和抛物线的综合运用,解题时要认真审题,注意抛物线性质的灵活运用,合理地进行等价转化.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
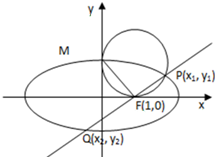 椭圆G:
椭圆G: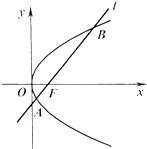 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A,B两点
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A,B两点