题目内容
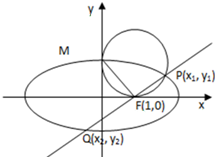 椭圆G:
椭圆G:| x2 |
| a2 |
| y2 |
| b2 |
| FA |
| FB |
(1)求椭圆C的标准方程;
(2)设椭圆G的上顶点为M,是否存在直线L,L交椭圆于P(x1,y1)、Q(x2,y2)两点,满足PQ⊥MF,且|PQ|=
| 4 |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据
•
=-1且|OF|=1,建立方程,求出几何量,即可得出椭圆C的标准方程;
(2)直线方程代入椭圆方程,利用韦达定理及弦长公式,即可求出直线L的方程.
| FA |
| FB |
(2)直线方程代入椭圆方程,利用韦达定理及弦长公式,即可求出直线L的方程.
解答:
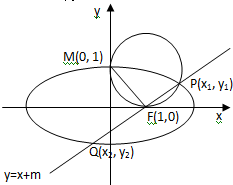 解:(1)∵
解:(1)∵
•
=-1且|OF|=1,
∴c=1,(a+c)(a-c)=1
∴a2=2b2=2-1=1
∴椭圆C的方程是
+y2=1┉┉┉┉┉┉(4分),
(2)设P(x1,y1) Q(x2,y2)(6分)
∵MF⊥PQ,∴设lPQ:y=x+m
由
得3x2+4mx+2m2-2=0
∴x1+x2=-
,x1x2=
┉┉┉┉┉┉(8分)
由|PQ|=
得
|x1-x2|=
,
∴(x1+x2)2-4x1x2=
,
∴
-
=
,
∴m=±
经检验m=±
时△>0
∴所求的直线方程是:y=x±
┉┉┉┉┉┉(12分)
 解:(1)∵
解:(1)∵| FA |
| FB |
∴c=1,(a+c)(a-c)=1
∴a2=2b2=2-1=1
∴椭圆C的方程是
| x2 |
| 2 |
(2)设P(x1,y1) Q(x2,y2)(6分)
∵MF⊥PQ,∴设lPQ:y=x+m
由
|
∴x1+x2=-
| 4m |
| 3 |
| 2m2-2 |
| 3 |
由|PQ|=
| 4 |
| 3 |
| 1+1 |
| 4 |
| 3 |
∴(x1+x2)2-4x1x2=
| 8 |
| 9 |
∴
| 16m2 |
| 9 |
| 8m2-8 |
| 3 |
| 8 |
| 9 |
∴m=±
| 2 |
| 2 |
∴所求的直线方程是:y=x±
| 2 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理及弦长公式,考查学生的计算能力,属于中档题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
若实数x,y满足不等式组
,则z=2x+3y的最大值是( )
|
| A、13 | B、12 | C、11 | D、10 |
 已知抛物线C的方程为
已知抛物线C的方程为 在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.
在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.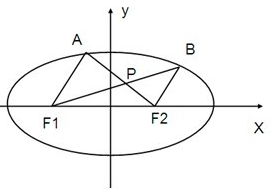 在椭圆
在椭圆