题目内容
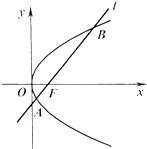 如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A,B两点
如图,已知抛物线C:y2=4x焦点为F,直线l经过点F且与抛物线C相交于A,B两点(Ⅰ)若线段AB的中点在直线y=1上,求直线l的方程;
(Ⅱ)若线段|AB|=20,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题设先求出F(1,0),设出斜率k,及A(x1,y1),B(x2,y2),由于本题知道了中点的坐标,故可将两点坐标代入用点差法建立k的方程求它的值.
(Ⅱ)先设出直线l的方程为x=my+1,与抛物线方程联立,利用弦长公式用参数m表示出弦长,再利用|AB|=20即可得出参数m的方程,解出它的值即可得出直线的方程.
(Ⅱ)先设出直线l的方程为x=my+1,与抛物线方程联立,利用弦长公式用参数m表示出弦长,再利用|AB|=20即可得出参数m的方程,解出它的值即可得出直线的方程.
解答:
解:(Ⅰ)由已知得交点坐标为F(1,0),…(1分)
设直线l的斜率为k,A(x1,y1),B(x2,y2),AB中点M(x0,y0)
则
,
⇒(y1+y2)(y1-y2)=4(x1-x2),
所以2y0k=4,又y0=1,所以k=2…(5分)
故直线l的方程是:y=2x-2…(6分)
(Ⅱ)设直线l的方程为x=my+1,…(7分)
与抛物线方程联立得
,
消元得y2-4my-4=0,…(8分)
所以有y1+y2=4m,y1y2=-4,△=16(m2+1)>0
…(10分)
所以有4(m2+1)=20,解得m=±2,…(12分)
所以直线l的方程是:x=±2y+1,即x±2y-1=0…(13分)
设直线l的斜率为k,A(x1,y1),B(x2,y2),AB中点M(x0,y0)
则
|
|
所以2y0k=4,又y0=1,所以k=2…(5分)
故直线l的方程是:y=2x-2…(6分)
(Ⅱ)设直线l的方程为x=my+1,…(7分)
与抛物线方程联立得
|
消元得y2-4my-4=0,…(8分)
所以有y1+y2=4m,y1y2=-4,△=16(m2+1)>0
|
所以有4(m2+1)=20,解得m=±2,…(12分)
所以直线l的方程是:x=±2y+1,即x±2y-1=0…(13分)
点评:本题考查了直线与圆锥曲线的综合问题考查了点差法求斜率的技巧,弦长公式,属于此类题中的常规题,本类题规律固定,都可用本题这样的方式求解

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
如图所示的程序框图,能使输入的x值与输出的y值相等的x值个数为( )
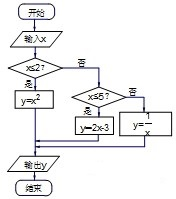

| A、1 | B、2 | C、3 | D、4 |
 已知抛物线C的方程为
已知抛物线C的方程为 在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.
在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x-3)2+(y-4)2=1.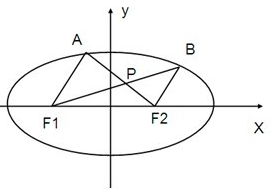 在椭圆
在椭圆