题目内容
设全集U是实数集R,集合M={x|x2>2x},N={x|log2(x-1)≤0},则(∁UM)∩N为( )
| A、{x|1<x<2} |
| B、{x|1≤x≤2} |
| C、{x|1<x≤2} |
| D、{x|1≤x<2} |
考点:交、并、补集的混合运算
专题:集合
分析:分别求出M与N中不等式的解集,确定出M与N,根据全集U=R,求出M的补集,找出M补集与N的交集即可.
解答:
解:由M中的不等式变形得:x2-2x>0,即x(x-2)>0,
解得:x>2或x<0,
∴M={x|x>2或x<0},
∵全集U=R,
∴∁UM={x|0≤x≤2},
由N中的不等式变形得:log2(x-1)≤0=log21,
得到0<x-1≤1,
解得:1<x≤2,即N={x|1<x≤2},

则(∁UM)∩N={x|1<x≤2}.
故选:C.
解得:x>2或x<0,
∴M={x|x>2或x<0},
∵全集U=R,
∴∁UM={x|0≤x≤2},
由N中的不等式变形得:log2(x-1)≤0=log21,
得到0<x-1≤1,
解得:1<x≤2,即N={x|1<x≤2},

则(∁UM)∩N={x|1<x≤2}.
故选:C.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若复数z满足(1+i)z=1+2i(其中i是虚数单位),则复数z对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知正方形ABCD,AB=2,AC、BD交点为O,在ABCD内随机取一点E,则点E满足OE<1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=lg(1+x)-lg(1-x) |
| C、f(x)=2x+2-x |
| D、f(x)=x3-1 |
 如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.
如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.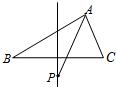 如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则
如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则