题目内容
已知椭圆5x2+9y2=45,椭圆的右焦点为F,
(1)求过点F且斜率为1的直线被椭圆截得的弦长;
(2)判断点A(1,1)与椭圆的位置关系,并求以A为中点椭圆的弦所在的直线方程.
(1)求过点F且斜率为1的直线被椭圆截得的弦长;
(2)判断点A(1,1)与椭圆的位置关系,并求以A为中点椭圆的弦所在的直线方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设出直线的方程,联立直线与椭圆的方程利用由弦长公式可得答案.
(2)设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),A(1,1)为EF中点,x1+x2=2,y1+y2=2,利用点差法能够求出以A(1,1)为中点椭圆的弦所在的直线方程.
(2)设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),A(1,1)为EF中点,x1+x2=2,y1+y2=2,利用点差法能够求出以A(1,1)为中点椭圆的弦所在的直线方程.
解答:
解:(1)由题意可得:过点F且斜率为1的直线方程为y=x-2,
联立直线与椭圆的方程可得:14x2-36x-9=0,
∴x1+x2=
,x1•x2=-
,
由弦长公式可得:|MN|=
•
=
(2)设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),
∵A(1,1)为EF中点,
∴x1+x2=2,y1+y2=2,
把E(x1,y1),F(x2,y2)分别代入椭圆5x2+9y2=45,
得5x12+9y12=45,5x22+9y22=45
∴5(x1+x2)(x1-x2)+9(y1+y2)(y1-y2)=0,
∴10(x1-x2)+18(y1-y2)=0,
∴k=
=-
,
∴以A(1,1)为中点椭圆的弦所在的直线方程为:y-1=-
(x-1),
整理,得5x+9y-14=0.
联立直线与椭圆的方程可得:14x2-36x-9=0,
∴x1+x2=
| 18 |
| 7 |
| 9 |
| 14 |
由弦长公式可得:|MN|=
| 1+1 |
(
|
| 30 |
| 7 |
(2)设以A(1,1)为中点椭圆的弦与椭圆交于E(x1,y1),F(x2,y2),
∵A(1,1)为EF中点,
∴x1+x2=2,y1+y2=2,
把E(x1,y1),F(x2,y2)分别代入椭圆5x2+9y2=45,
得5x12+9y12=45,5x22+9y22=45
∴5(x1+x2)(x1-x2)+9(y1+y2)(y1-y2)=0,
∴10(x1-x2)+18(y1-y2)=0,
∴k=
| y1-y2 |
| x1-x2 |
| 5 |
| 9 |
∴以A(1,1)为中点椭圆的弦所在的直线方程为:y-1=-
| 5 |
| 9 |
整理,得5x+9y-14=0.
点评:本题主要考查了椭圆的应用,考查了弦长问题与弦中点问题,正确运用点差法是关键.

练习册系列答案
相关题目
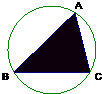 如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )
如图已知圆的半径为10,其内接三角形ABC的内角A、B分别为60°和45°,现向圆内随机撒一粒豆子,则豆子落在三角形ABC内的概率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
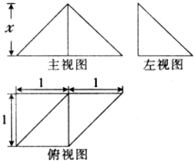 如图所示是一个几何体的三视图,若该几何体的体积为
如图所示是一个几何体的三视图,若该几何体的体积为| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
若复数z满足(1+i)z=1+2i(其中i是虚数单位),则复数z对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.
如图,有一条光线沿直线y=4射到抛物线y2=4x上的一点P,经抛物线反射后,反射光线与抛物线的交于另一点Q,O是抛物线的顶点,F是抛物线的焦点,求弦PQ的斜率和△OPQ的面积.