题目内容
关于函数f(x)=
给出下列四个命题:
①当x>0时,y=f(x)单调递减且没有最值;
②方程f(x)=kx+b(k≠0)一定有解;
③如果方程f(x)=k有解,则解的个数一定是偶数;
④y=f(x)是偶函数且有最小值.则其中真命题是 .(只要写标题号)
| |x| |
| |x|-1 |
①当x>0时,y=f(x)单调递减且没有最值;
②方程f(x)=kx+b(k≠0)一定有解;
③如果方程f(x)=k有解,则解的个数一定是偶数;
④y=f(x)是偶函数且有最小值.则其中真命题是
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:①x>0时,由x≠1知y=f(x)不具有单调性,判定命题错误;
②函数f(x)=
是偶函数,在x>0且k>0时,判定函数y=f(x)与y=kx在第一象限内有交点;由对称性知,x<0且k>0时,函数y=f(x)与y=kx在第二象限内有交点;得方程f(x)=kx+b(k≠0)有解;
③函数f(x)=
是偶函数,且f(x)=0,举例说明k=0时,方程f(x)=k有1个解;
④函数f(x)=
是偶函数,画出函数的图象,即可判断结论是否正确.
②函数f(x)=
| |x| |
| |x|-1 |
③函数f(x)=
| |x| |
| |x|-1 |
④函数f(x)=
| |x| |
| |x|-1 |
解答:
解:①当x>0时,y=f(x)=
=1+
在区间(0,1)和(1,+∞)上分别是单调递减的函数,且无最值;
∴命题①错误;
②函数f(x)=
是偶函数,当x>0时,y=f(x)=
=1+
在区间(0,1)和(1,+∞)上分别是单调递减的函数;
当k>0时,函数y=f(x)与y=kx在第一象限内一定有交点;
由对称性知,当x<0且k>0时,函数y=f(x)与y=kx在第二象限内一定有交点;
∴方程f(x)=kx+b(k≠0)一定有解;
∴命题②正确;
③∵函数f(x)=
是偶函数,且f(x)=0当k=0时,函数y=f(x)与y=k的图象只有一个交点,∴方程f(x)=k的解的个数是奇数;∴命题③错误;
④∵函数f(x)=
是偶函数,x≠±1,
x>0时,y=f(x)=
=1+
在区间(0,1)和(1,+∞)上分别是单调递减的函数;
由对称性知,x<0时,y=f(x)=
=1-
在区间(-∞,-1)和(-1,0)上分别是单调递增的函数;
如图所示,
∴函数f(x)无最小值,命题④错误.
故答案为:②.
| x |
| x-1 |
| 1 |
| x-1 |
∴命题①错误;
②函数f(x)=
| |x| |
| |x|-1 |
| x |
| x-1 |
| 1 |
| x-1 |
当k>0时,函数y=f(x)与y=kx在第一象限内一定有交点;
由对称性知,当x<0且k>0时,函数y=f(x)与y=kx在第二象限内一定有交点;
∴方程f(x)=kx+b(k≠0)一定有解;
∴命题②正确;
③∵函数f(x)=
| |x| |
| |x|-1 |
④∵函数f(x)=
| |x| |
| |x|-1 |
x>0时,y=f(x)=
| x |
| x-1 |
| 1 |
| x-1 |
由对称性知,x<0时,y=f(x)=
| -x |
| -x-1 |
| 1 |
| x+1 |
如图所示,

∴函数f(x)无最小值,命题④错误.
故答案为:②.
点评:本题考查了含有绝对值的分式函数的图象与性质的问题,解题时应先去掉绝对值,化为分段函数,把分式函数分离常数,是易错题.

练习册系列答案
相关题目
若复数z满足(1+i)z=1+2i(其中i是虚数单位),则复数z对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=lg(1+x)-lg(1-x) |
| C、f(x)=2x+2-x |
| D、f(x)=x3-1 |
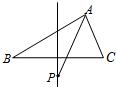 如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则
如图,△ABC中,|AB|=4,|AC|=3,若P为线段BC的垂直平分线上的动点,则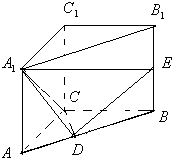 已知直三棱柱ABC-A1B1C1中,∠ACB=
已知直三棱柱ABC-A1B1C1中,∠ACB=