Question

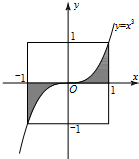如图，设D是图中边长为2的正方形区域，E是函数y=x³的图象与x轴及x=±1围成的阴影区域．向D中随机投一点，则该点落入E中的概率为（　　）

• A、

  1

  16

• B、

  1

  8

• C、

  1

  4

• D、

  1

  2

Answer 1

考点：几何概型

专题：概率与统计

分析：根据积分的公式计算出区域E的面积，利用几何概型的概率公式即可得到结论．

解答： 解：根据积分的几何意义可知区域E的面积S=2

∫

1 0

x3dx=2×

1

4

x4

|

1 0

=2×

1

4

=

1

2

，
区域D的面积为S₁=2×2=4，
∴根据几何概型的概率公式可知所求概率P=

S

S1

=

1 2

4

=

1

8

，
故选：B．

点评：本题主要考查几何概型的概率计算，根据积分的几何意义求出对应区域的面积是解决本题的关键．