Question

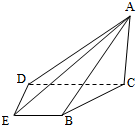如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=

2

．
（Ⅰ）证明：DE⊥平面ACD；
（Ⅱ）求二面角B-AD-E的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面垂直的判定

专题：空间位置关系与距离,空间角,立体几何

分析：（Ⅰ）依题意，易证AC⊥平面BCDE，于是可得AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；
（Ⅱ）作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AE交于点G，连接BG，由（Ⅰ）知DE⊥AD，则FG⊥AD，所以∠BFG就是二面角B-AD-E的平面角，利用题中的数据，解三角形，可求得BF=

2 3

3

，AF=

2

3

AD，从而GF=

2

3

，cos∠BFG=

GF2+BF2-BG2

2BF•GF

=

3

2

，从而可求得答案．

解答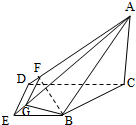： 证明：（Ⅰ）在直角梯形BCDE中，由DE=BE=1，CD=2，得BD=BC=

2

，
由AC=

2

，AB=2得AB²=AC²+BC²，即AC⊥BC，
又平面ABC⊥平面BCDE，从而AC⊥平面BCDE，
所以AC⊥DE，又DE⊥DC，从而DE⊥平面ACD；
（Ⅱ）作BF⊥AD，与AD交于点F，过点F作FG∥DE，与AE交于点G，连接BG，由（Ⅰ）知DE⊥AD，则FG⊥AD，所以∠BFG就是二面角B-AD-E的平面角，在直角梯形BCDE中，由CD²=BC²+BD²，得BD⊥BC，
又平面ABC⊥平面BCDE，得BD⊥平面ABC，从而BD⊥AB，
由于AC⊥平面BCDE，得AC⊥CD．
在Rt△ACD中，由DC=2，AC=

2

，得AD=

6

；
在Rt△AED中，由ED=1，AD=

6

得AE=

7

；
在Rt△ABD中，由BD=

2

，AB=2，AD=

6

得BF=

2 3

3

，AF=

2

3

AD，从而GF=

2

3

，
在△ABE，△ABG中，利用余弦定理分别可得cos∠BAE=

5 7

14

，BG=

2

3

．
在△BFG中，cos∠BFG=

GF2+BF2-BG2

2BF•GF

=

3

2

，
所以，∠BFG=

π

6

，二面角B-AD-E的大小为

π

6

．

点评：本题主要考查空间点、线、面位置关系，二面角等基础知识，同时考查空间想象能力，推理论证能力和运算求解能力．