题目内容
设椭圆
+
=1(a>b>0)的左、右焦点分别为F1、F2,右顶点为A,上顶点为B,已知|AB|=
|F1F2|.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过原点O的直线l与该圆相切,求直线l的斜率.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆的离心率;
(Ⅱ)设P为椭圆上异于其顶点的一点,以线段PB为直径的圆经过点F1,经过原点O的直线l与该圆相切,求直线l的斜率.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设椭圆的右焦点为F2(c,0),由|AB|=
|F1F2|.可得
=
×2c,再利用b2=a2-c2,e=
即可得出.
(Ⅱ)由(Ⅰ)可得b2=c2.可设椭圆方程为
+
=1,设P(x0,y0),由F1(-c,0),B(0,c),可得
,
.利用圆的性质可得
⊥
,于是
•
=0,得到x0+y0+c=0,由于点P在椭圆上,可得
+
=1.联立可得3
+4cx0=0,解得P(-
c,
).设圆心为T(x1,y1),利用中点坐标公式可得T(-
c,
c),利用两点间的距离公式可得圆的半径r.设直线l的方程为:y=kx.利用直线与圆相切的性质即可得出.
| ||
| 2 |
| a2+b2 |
| ||
| 2 |
| c |
| a |
(Ⅱ)由(Ⅰ)可得b2=c2.可设椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
| F1P |
| F1B |
| F1B |
| F1P |
| F1B |
| F1P |
| ||
| 2c2 |
| ||
| c2 |
| x | 2 0 |
| 4 |
| 3 |
| c |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:
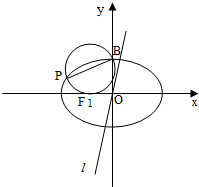 解:(Ⅰ)设椭圆的右焦点为F2(c,0),
解:(Ⅰ)设椭圆的右焦点为F2(c,0),
由|AB|=
|F1F2|,可得
=
×2c,化为a2+b2=3c2.
又b2=a2-c2,∴a2=2c2.
∴e=
=
.
(Ⅱ)由(Ⅰ)可得b2=c2.因此椭圆方程为
+
=1.
设P(x0,y0),由F1(-c,0),B(0,c),可得
=(x0+c,y0),
=(c,c).
∵
⊥
,
∴
•
=c(x0+c)+cy0=0,
∴x0+y0+c=0,
∵点P在椭圆上,∴
+
=1.
联立
,化为3
+4cx0=0,
∵x0≠0,∴x0=-
c,
代入x0+y0+c=0,可得y0=
.
∴P(-
c,
).
设圆心为T(x1,y1),则x1=
=-
c,y1=
=
c.
∴T(-
c,
c),
∴圆的半径r=
=
c.
设直线l的斜率为k,则直线l的方程为:y=kx.
∵直线l与圆相切,
∴
=
c,
整理得k2-8k+1=0,解得k=4±
.
∴直线l的斜率为4±
.
 解:(Ⅰ)设椭圆的右焦点为F2(c,0),
解:(Ⅰ)设椭圆的右焦点为F2(c,0),由|AB|=
| ||
| 2 |
| a2+b2 |
| ||
| 2 |
又b2=a2-c2,∴a2=2c2.
∴e=
| c |
| a |
| ||
| 2 |
(Ⅱ)由(Ⅰ)可得b2=c2.因此椭圆方程为
| x2 |
| 2c2 |
| y2 |
| c2 |
设P(x0,y0),由F1(-c,0),B(0,c),可得
| F1P |
| F1B |
∵
| F1B |
| F1P |
∴
| F1B |
| F1P |
∴x0+y0+c=0,
∵点P在椭圆上,∴
| ||
| 2c2 |
| ||
| c2 |
联立
|
| x | 2 0 |
∵x0≠0,∴x0=-
| 4 |
| 3 |
代入x0+y0+c=0,可得y0=
| c |
| 3 |
∴P(-
| 4 |
| 3 |
| c |
| 3 |
设圆心为T(x1,y1),则x1=
-
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 2 |
| 3 |
∴T(-
| 2 |
| 3 |
| 2 |
| 3 |
∴圆的半径r=
(-
|
| ||
| 3 |
设直线l的斜率为k,则直线l的方程为:y=kx.
∵直线l与圆相切,
∴
|-
| ||||
|
| ||
| 3 |
整理得k2-8k+1=0,解得k=4±
| 15 |
∴直线l的斜率为4±
| 15 |
点评:本题中考查了椭圆与圆的标准方程及其性质、点与椭圆的位置关系、直线与圆相切问题、点到直线的距离公式、中点坐标公式等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
下列函数中,与函数y=x的奇偶性,单调性均相同的是( )
| A、y=x2 | ||
| B、y=sinx | ||
| C、y=lnx | ||
D、y=
|
已知等差数列{an}的前n项和为Sn,且a6=1,则S11的值为( )
| A、11 | B、10 | C、12 | D、1 |
从正方体六个面的对角线中任取两条作为一对.其中所成的角为60°的共有( )
| A、24对 | B、30对 |
| C、48对 | D、60对 |
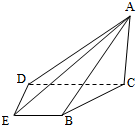 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= 已知椭圆
已知椭圆