题目内容
已知集合M={y|y=1+
}，N={y|y=ln（x2+1）}，则M∩N=（ ）
| 1 | ||
|
| A、（0，+∞） |
| B、[0，+∞） |
| C、（1，+∞） |
| D、[1，+∞） |
考点：交集及其运算,对数函数的单调性与特殊点
专题：集合
分析：根据函数的性质求出集合，M，N．利用集合的基本运算即可得到结论．
解答：
解：M={y|y=1+
}={y|y＞1}，N={y|y=ln（x2+1）}={y|y=ln（x2+1）≥0}，
则M∩N={y|y＞1}，
故选：C．
| 1 | ||
|
则M∩N={y|y＞1}，
故选：C．
点评：本题主要考查集合的基本运算，根据函数的性质求出相应的值域是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知集合U={1，2，3，4}，集合A={2，3}，B={3，4}，则∁U（A∪B）=（ ）
| A、{1，2，4} | B、{2，4} |
| C、={3} | D、{1} |
下列函数中，与函数y=x的奇偶性，单调性均相同的是（ ）
| A、y=x2 | ||
| B、y=sinx | ||
| C、y=lnx | ||
D、y=
|
复数
的共轭复数是（ ）
| 5 |
| 3-4i |
A、
| ||||
B、
| ||||
| C、3+4i | ||||
| D、3-4i |
函数f（x）=Asinx+Bcosx（A，B∈R且不全为零），则“B=0”是“函数f（x）为奇函数的”（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知Sn是等差数列{an}（n∈N*）的前n项和，且S8＞S9＞S7，有下列四个命题，期中是假命题的是（ ）
| A、公差d＜0 |
| B、在所有Sn＜0中，S17最大 |
| C、a8＞a9 |
| D、满足Sn＞0的n的个数有15个 |
已知等差数列{an}的前n项和为Sn，且a6=1，则S11的值为（ ）
| A、11 | B、10 | C、12 | D、1 |
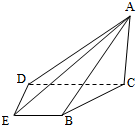如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=