题目内容
 如图,曲线段OC是函数y=
如图,曲线段OC是函数y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:由y=
与y=x-2,联立可得C(4,2),求出正方形ABCD的面积、阴影部分的面积,以面积为测度,即可求出概率.
| x |
解答:
解:由y=
与y=x-2,联立可得C(4,2),故正方形ABCD的面积为16,
阴影部分的面积S=
(
-x+2)dx=(
x
-
x2+2x)
=
,
∴落入区域E中的概率为
=
.
故选:C.
| x |
阴影部分的面积S=
| ∫ | 4 0 |
| x |
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
| | | 4 0 |
| 16 |
| 3 |
∴落入区域E中的概率为
| ||
| 16 |
| 1 |
| 3 |
故选:C.
点评:本题考查的知识点是几何概型,其中利用积分公式计算出阴影部分的面积是解答本题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知集合U={1,2,3,4},集合A={2,3},B={3,4},则∁U(A∪B)=( )
| A、{1,2,4} | B、{2,4} |
| C、={3} | D、{1} |
某学生默写英语单词“tomorrow”,他记得这个单词由3个“o”,2个“r”,t,w,m各一个组成,三个“o”不相邻且不在首位,两个“r”相邻,则他按此结论可写出多少个不同的字母顺序( )
| A、576 | B、240 |
| C、168 | D、96 |
若复数z=-
+
i,则z2的共轭复数为( )
| 1 |
| 2 |
| ||
| 2 |
A、-
| ||||||
B、-
| ||||||
| C、-1 | ||||||
| D、1 |
在等差数列{an}中,首项a1=0,公差d≠0,若ap=S9,则p的值为( )
| A、37 | B、20 | C、36 | D、9 |
下列函数中,与函数y=x的奇偶性,单调性均相同的是( )
| A、y=x2 | ||
| B、y=sinx | ||
| C、y=lnx | ||
D、y=
|
复数
的共轭复数是( )
| 5 |
| 3-4i |
A、
| ||||
B、
| ||||
| C、3+4i | ||||
| D、3-4i |
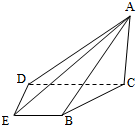 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=