题目内容
已知函数f（x）=
的定义域为[0，+∞），则实数a的取值范围为（ ）
| ||
| x3-3x+a |
| A、（0，3） |
| B、（0，2） |
| C、（2，+∞） |
| D、（3，+∞） |
考点：利用导数研究函数的极值
专题：导数的综合应用
分析：根据函数的定义域，可得分母x≥0时，x3-3x+a≠0，然后利用导数进行求解即可．
解答：
解：∵f（x）=
的定义域为[0，+∞），
∴当x≥0时，x3-3x+a≠0，
设f（x）=x3-3x+a，f′（x）=3x2-3=3（x2-1），
则当x＞1时，f′（x）＞0，函数单调递增，
当-1＜x＜1时，f′（x）＜0，函数单调递减，
即当x=1时，函数f（x）取得极小值f（1）=a-2，
要使x≥0时，x3-3x+a≠0，
则f（1）=a-2＞0，即可，解得a＞2，
即实数a的取值范围为（2，+∞），
故选：C
| ||
| x3-3x+a |
∴当x≥0时，x3-3x+a≠0，
设f（x）=x3-3x+a，f′（x）=3x2-3=3（x2-1），
则当x＞1时，f′（x）＞0，函数单调递增，
当-1＜x＜1时，f′（x）＜0，函数单调递减，
即当x=1时，函数f（x）取得极小值f（1）=a-2，
要使x≥0时，x3-3x+a≠0，
则f（1）=a-2＞0，即可，解得a＞2，
即实数a的取值范围为（2，+∞），
故选：C
点评：本题主要考查函数定义域的应用，根据函数的定义域确定分母不为零，利用导数求出函数的极值是解决本题的关键，综合性较强．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
某学生默写英语单词“tomorrow”，他记得这个单词由3个“o”，2个“r”，t，w，m各一个组成，三个“o”不相邻且不在首位，两个“r”相邻，则他按此结论可写出多少个不同的字母顺序（ ）
| A、576 | B、240 |
| C、168 | D、96 |
复数
的共轭复数是（ ）
| 5 |
| 3-4i |
A、
| ||||
B、
| ||||
| C、3+4i | ||||
| D、3-4i |
已知Sn是等差数列{an}（n∈N*）的前n项和，且S8＞S9＞S7，有下列四个命题，期中是假命题的是（ ）
| A、公差d＜0 |
| B、在所有Sn＜0中，S17最大 |
| C、a8＞a9 |
| D、满足Sn＞0的n的个数有15个 |
已知等差数列{an}的前n项和为Sn，且a6=1，则S11的值为（ ）
| A、11 | B、10 | C、12 | D、1 |
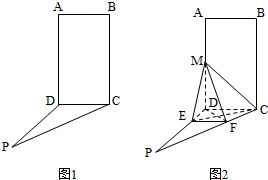如图1，四边形ABCD为矩形，PD⊥平面ABCD，AB=1，BC=PC=2作如图2折叠；折痕EF∥DC，其中点E，F分别在线段PD，PC上，沿EF折叠后点P叠在线段AD上的点记为M，并且MF⊥CF．
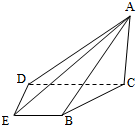如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=
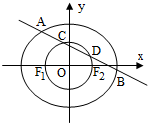已知椭圆