题目内容
 如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
如图,三棱柱ABC-A1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.(Ⅰ)证明:AC=AB1;
(Ⅱ)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角A-A1B1-C1的余弦值.
考点:用空间向量求平面间的夹角,空间向量的夹角与距离求解公式
专题:空间向量及应用
分析:(1)连结BC1,交B1C于点O,连结AO,可证B1C⊥平面ABO,可得B1C⊥AO,B10=CO,进而可得AC=AB1;
(2)以O为坐标原点,
的方向为x轴的正方向,|
|为单位长度,
的方向为y轴的正方向,
的方向为z轴的正方向建立空间直角坐标系,分别可得两平面的法向量,可得所求余弦值.
(2)以O为坐标原点,
| OB |
| OB |
| OB1 |
| OA |
解答:
解:(1)连结BC1,交B1C于点O,连结AO,
∵侧面BB1C1C为菱形,
∴BC1⊥B1C,且O为BC1和B1C的中点,
又∵AB⊥B1C,∴B1C⊥平面ABO,
∵AO?平面ABO,∴B1C⊥AO,
又B10=CO,∴AC=AB1,
(2)∵AC⊥AB1,且O为B1C的中点,∴AO=CO,
又∵AB=BC,∴△BOA≌△BOC,∴OA⊥OB,
∴OA,OB,OB1两两垂直,
以O为坐标原点,
的方向为x轴的正方向,|
|为单位长度,
的方向为y轴的正方向,
的方向为z轴的正方向建立空间直角坐标系,
∵∠CBB1=60°,∴△CBB1为正三角形,又AB=BC,
∴A(0,0,
),B(1,0,0,),B1(0,
,0),C(0,-
,0)
∴
=(0,
,-
),
=
=(1,0,-
),
=
=(-1,-
,0),
设向量
=(x,y,z)是平面AA1B1的法向量,
则
,可取
=(1,
,
),
同理可得平面A1B1C1的一个法向量
=(1,-
,
),
∴cos<
,
>=
=
,
∴二面角A-A1B1-C1的余弦值为
∵侧面BB1C1C为菱形,
∴BC1⊥B1C,且O为BC1和B1C的中点,
又∵AB⊥B1C,∴B1C⊥平面ABO,
∵AO?平面ABO,∴B1C⊥AO,
又B10=CO,∴AC=AB1,
(2)∵AC⊥AB1,且O为B1C的中点,∴AO=CO,
又∵AB=BC,∴△BOA≌△BOC,∴OA⊥OB,
∴OA,OB,OB1两两垂直,
以O为坐标原点,
| OB |
| OB |
| OB1 |
| OA |
∵∠CBB1=60°,∴△CBB1为正三角形,又AB=BC,
∴A(0,0,
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴
| AB1 |
| ||
| 3 |
| ||
| 3 |
| A1B1 |
| AB |
| ||
| 3 |
| B1C1 |
| BC |
| ||
| 3 |
设向量
| n |
则
|
| n |
| 3 |
| 3 |
同理可得平面A1B1C1的一个法向量
| m |
| 3 |
| 3 |
∴cos<
| m |
| n |
| ||||
|
|
| 1 |
| 7 |
∴二面角A-A1B1-C1的余弦值为
| 1 |
| 7 |
点评:本题考查空间向量法解决立体几何问题,建立坐标系是解决问题的关键,属中档题.

练习册系列答案
相关题目
若复数z=-
+
i,则z2的共轭复数为( )
| 1 |
| 2 |
| ||
| 2 |
A、-
| ||||||
B、-
| ||||||
| C、-1 | ||||||
| D、1 |
函数f(x)=Asinx+Bcosx(A,B∈R且不全为零),则“B=0”是“函数f(x)为奇函数的”( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知等差数列{an}的前n项和为Sn,且a6=1,则S11的值为( )
| A、11 | B、10 | C、12 | D、1 |
首项为1,公差不为0的等差数列{an}中,a3、a4、a6是一个等比数列的前三项,则这个等比数列的第四项是( )
| A、8 | B、-8 | C、-6 | D、不确定 |
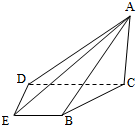 如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=
如图,在四棱锥A-BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC=