题目内容
已知函数f(x)=ax+lnx,g(x)=ex.
(1)求函数f(x)在点(1,f(1))处且倾斜角为
的切线方程;
(2)若不等式g(x)<
有解,求实数m的取值范围;
(3)定义:对于函数y=f(x)和y=g(x)在其公共定义域内的任意实数x0,称|f(x0)-g(x0)|的值为两函数在x0处的差值.证明:当a=0时,函数y=f(x)和y=g(x)在其公共定义域内的所有差值都大于2.
(1)求函数f(x)在点(1,f(1))处且倾斜角为
| π |
| 3 |
(2)若不等式g(x)<
| x+m | ||
|
(3)定义:对于函数y=f(x)和y=g(x)在其公共定义域内的任意实数x0,称|f(x0)-g(x0)|的值为两函数在x0处的差值.证明:当a=0时,函数y=f(x)和y=g(x)在其公共定义域内的所有差值都大于2.
考点:利用导数研究曲线上某点切线方程,利用导数求闭区间上函数的最值
专题:综合题,导数的综合应用
分析:(1)利用函数f(x)在点(1,f(1))处且倾斜角为
,先求出a的值,即可求出切线方程;
(2)由题意:ex<
有解,即ex
<x+m有解,因此只需m>ex
-x,x∈(0,+∞)有解即可;
(3)|f(x)-g(x)|=|ln x-ex|=ex-ln x=ex-x-(ln x-x),设m(x)=ex-x,x∈(0,+∞),n(x)=ln x-x,x∈(0,+∞),分别确定函数的范围,即可得出结论.
| π |
| 3 |
(2)由题意:ex<
| x+m | ||
|
| x |
| x |
(3)|f(x)-g(x)|=|ln x-ex|=ex-ln x=ex-x-(ln x-x),设m(x)=ex-x,x∈(0,+∞),n(x)=ln x-x,x∈(0,+∞),分别确定函数的范围,即可得出结论.
解答:
(1)解:f(x)的定义域是(0,+∞),f′(x)=a+
(x>0),…(1分)
∴k=f′(1)=a+1=
,
∴a=
-1…(2分)
∵f(1)=
-1 …(3分)
∴切线为y=
x-1;…(4分)
(2)解:由题意:ex<
有解,即ex
<x+m有解,
因此只需m>ex
-x,x∈(0,+∞)有解即可.…(5分)
设h(x)=ex
-x,h′(x)=ex
+
-1=ex(
+
)-1,…(6分)
∵
+
≥
>1,且x∈(0,+∞)时ex>1,
∴ex(
+
)-1>0,即h′(x)>0,故h(x)在(0,+∞)上单调增函数,…(7分)
∴h(x)>h(0)=0,故m>0.…(8分)
(3)证明:当a=0时,f(x)=ln x,f(x)与g(x)的公共定义域为(0,+∞),
|f(x)-g(x)|=|ln x-ex|=ex-ln x=ex-x-(ln x-x),…(9分)
设m(x)=ex-x,x∈(0,+∞).
∵m′(x)=ex-1>0,m(x)在(0,+∞)上单调递增,m(x)>m(0)=1,…(10分)
又设n(x)=ln x-x,x∈(0,+∞),n′(x)=
-1,
当x∈(0,1)时,n′(x)>0,n(x)单调递增,
当x∈(1,+∞)时,n′(x)<0,n(x)单调递减,
∴x=1为n(x)的极大值点,即n(x)≤n(1)=-1,…(11分)
故|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2.
即公共定义域内任一点差值都大于2.…(12分)
| 1 |
| x |
∴k=f′(1)=a+1=
| 3 |
∴a=
| 3 |
∵f(1)=
| 3 |
∴切线为y=
| 3 |
(2)解:由题意:ex<
| x+m | ||
|
| x |
因此只需m>ex
| x |
设h(x)=ex
| x |
| x |
| ex | ||
2
|
| x |
| 1 | ||
2
|
∵
| x |
| 1 | ||
2
|
| 2 |
∴ex(
| x |
| 1 | ||
2
|
∴h(x)>h(0)=0,故m>0.…(8分)
(3)证明:当a=0时,f(x)=ln x,f(x)与g(x)的公共定义域为(0,+∞),
|f(x)-g(x)|=|ln x-ex|=ex-ln x=ex-x-(ln x-x),…(9分)
设m(x)=ex-x,x∈(0,+∞).
∵m′(x)=ex-1>0,m(x)在(0,+∞)上单调递增,m(x)>m(0)=1,…(10分)
又设n(x)=ln x-x,x∈(0,+∞),n′(x)=
| 1 |
| x |
当x∈(0,1)时,n′(x)>0,n(x)单调递增,
当x∈(1,+∞)时,n′(x)<0,n(x)单调递减,
∴x=1为n(x)的极大值点,即n(x)≤n(1)=-1,…(11分)
故|f(x)-g(x)|=m(x)-n(x)>1-(-1)=2.
即公共定义域内任一点差值都大于2.…(12分)
点评:本题考查利用导数研究曲线上某点切线方程,考查函数的单调性与极值,考查学生分析解决问题的能力,有难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

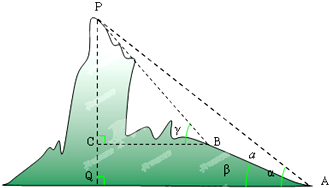 如图,在山脚A测得出山顶P的仰角为α,沿倾斜角为β的斜坡向上走a米到B,在B处测得山顶P的仰角为γ,求证:山高h=
如图,在山脚A测得出山顶P的仰角为α,沿倾斜角为β的斜坡向上走a米到B,在B处测得山顶P的仰角为γ,求证:山高h=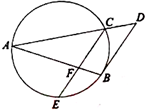 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为