题目内容
已知函数f(x)=|x-1|.
(Ⅰ)解不等式f(x-1)+f(1-x)≤2;
(Ⅱ)若a<0.求证:f(ax)-af(x)≥f(x).
(Ⅰ)解不等式f(x-1)+f(1-x)≤2;
(Ⅱ)若a<0.求证:f(ax)-af(x)≥f(x).
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)依题意,f(x-1)+f(1-x)≤2?|x-2|+|x|≤2,通过对x≤0与0<x<2及x≥2的讨论分析,去掉绝对值符号,即可求得原不等式的解集;
(Ⅱ)利用绝对值不等式,a<0时,可得f(ax)-af(x)=|ax-1|-a|x-1|≥|ax-1-ax+a|=|a-1|=f(a),从而可证结论.
(Ⅱ)利用绝对值不等式,a<0时,可得f(ax)-af(x)=|ax-1|-a|x-1|≥|ax-1-ax+a|=|a-1|=f(a),从而可证结论.
解答:
解:(Ⅰ)∵f(x-1)+f(1-x)=|x-2|+|x|.
因此只须解不等式|x-2|+|x|≤2.
当x≤0时,原不式等价于2-x-x≤2,即x≥0,所以x=0.
当0<x<2时,原不式等价于2≤2成立,所以0<x<2.
当x≥2时,原不式等价于x-2+x≤2,即x≤2,所以x=2.
综上,原不等式的解集为{x|0≤x≤2}.…(5分)
(Ⅱ)∵f(ax)-af(x)=|ax-1|-a|x-1|,
又a<0时,|ax-1|-a|x-1|=|ax-1|+|-ax+a|≥|ax-1-ax+a|=|a-1|=f(a),
∴a<0时,f(ax)-af(x)≥f(x).…(10分)
因此只须解不等式|x-2|+|x|≤2.
当x≤0时,原不式等价于2-x-x≤2,即x≥0,所以x=0.
当0<x<2时,原不式等价于2≤2成立,所以0<x<2.
当x≥2时,原不式等价于x-2+x≤2,即x≤2,所以x=2.
综上,原不等式的解集为{x|0≤x≤2}.…(5分)
(Ⅱ)∵f(ax)-af(x)=|ax-1|-a|x-1|,
又a<0时,|ax-1|-a|x-1|=|ax-1|+|-ax+a|≥|ax-1-ax+a|=|a-1|=f(a),
∴a<0时,f(ax)-af(x)≥f(x).…(10分)
点评:本题考查绝对值不等式的解法,通过对x≤0与0<x<2及x≥2的讨论分析,去掉绝对值符号是关键,考查转化思想与运算求解能力,属于中档题.

练习册系列答案
相关题目

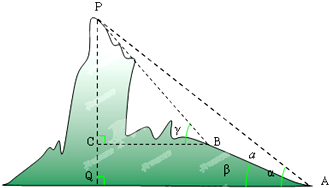 如图,在山脚A测得出山顶P的仰角为α,沿倾斜角为β的斜坡向上走a米到B,在B处测得山顶P的仰角为γ,求证:山高h=
如图,在山脚A测得出山顶P的仰角为α,沿倾斜角为β的斜坡向上走a米到B,在B处测得山顶P的仰角为γ,求证:山高h=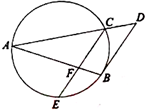 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为