题目内容
函数f(x)=3sin(2x-
)的图象为C,则如下结论中正确的序号是
①图象C关于直线x=
π对称;
②图象C关于点(
,0)对称;
③函数f(x)的最小正周期是π;
④由y=3sin2x的图角向右平移
个单位长度可以得到图象C.
| π |
| 3 |
①图象C关于直线x=
| 11 |
| 12 |
②图象C关于点(
| 2π |
| 3 |
③函数f(x)的最小正周期是π;
④由y=3sin2x的图角向右平移
| π |
| 3 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:通过求f(
π),f(
)的值判断命题①②的真假;
直接由周期公式求周期判断③的真假;
直接利用函数图象的平移求得y=3sin2x的图象向右平移
个单位长度所得图象的解析式判断④.
| 11 |
| 12 |
| 2π |
| 3 |
直接由周期公式求周期判断③的真假;
直接利用函数图象的平移求得y=3sin2x的图象向右平移
| π |
| 3 |
解答:
解:对于①,∵f(
π)=3sin(2×
π-
)=3sin
=-3,
∴图象C关于直线x=
π对称.
命题①正确;
对于②,∵f(
)=3sin(2×
-
)=3sinπ=0,
∴图象C关于点(
,0)对称.
命题②正确;
对于③,∵T=
=π,
∴函数f(x)的最小正周期是π.
命题③正确;
对于④,y=3sin2x的图象向右平移
个单位长度,得到:
y=sin[2(x-
)-
]=-sin2x.
命题④错误.
∴正确命题的序号是①②③.
故答案为:①②③.
| 11 |
| 12 |
| 11 |
| 12 |
| π |
| 3 |
| 3π |
| 2 |
∴图象C关于直线x=
| 11 |
| 12 |
命题①正确;
对于②,∵f(
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
∴图象C关于点(
| 2π |
| 3 |
命题②正确;
对于③,∵T=
| 2π |
| 2 |
∴函数f(x)的最小正周期是π.
命题③正确;
对于④,y=3sin2x的图象向右平移
| π |
| 3 |
y=sin[2(x-
| π |
| 3 |
| π |
| 3 |
命题④错误.
∴正确命题的序号是①②③.
故答案为:①②③.
点评:本题考查了y=Asin(ωx+φ)的图象的变换,训练了y=Asin(ωx+φ)型函数的对称轴、对称中心的求法,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
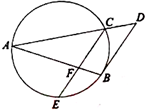 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D,过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=6,FB=2,EF=3,则线段CD的长为