题目内容
关于x的方程2x2+3ax+a2-a=0(a∈R)至少有一个模为1的根,求实数a的值.
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:①若两根为实根时,由条件求得a的值;②若两根为虚根时,再由条件求得a的值,综合可得结论.
解答:
解:①若两根为实根时,不妨设|x1|=1,则x1=±1,
当x1=1时,∴a2+2a+2=0,由于△<0可得a无解.
当x1=-1时,∴a2-4a+2=0,求得a=2±
.
②若两根为虚根时,则 x1=
x1•x2=| x1|2=1,即
=1,求得a=2,或 a=-1.
再根据此时△<0 可得a=-1.
综上可得,a=2±
,或 a=-1.
当x1=1时,∴a2+2a+2=0,由于△<0可得a无解.
当x1=-1时,∴a2-4a+2=0,求得a=2±
| 2 |
②若两根为虚根时,则 x1=
. |
| x2 |
| a2-a |
| 2 |
再根据此时△<0 可得a=-1.
综上可得,a=2±
| 2 |
点评:本题主要考查实系数一元二次方程求解的方法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
设f(x)是定义在R上的奇函数,且f(x+3)•f(x)=-1,f(-1)=2,则f(2008)=( )
| A、0.5 | B、0 | C、2 | D、-1 |
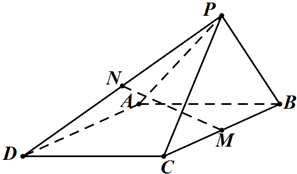 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.