题目内容
2014年男足世界杯在巴西举行,为了争夺最后一个小组赛参赛名额,甲、乙、丙三支国家队要进行比赛,根据规则:每两支队比赛一场,共赛三场;每场比赛胜者得3分,负者得0分,没有平局,获得第一名的队伍将夺得这个参赛名额.甲胜乙的概率为
,甲胜丙的概率为
,乙胜丙的概率为
.
(1)求甲获第一名且丙获第二名的概率:
(2)设在该次比赛中,丙得分为ξ,求ξ的分布列和数学期望.
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
(1)求甲获第一名且丙获第二名的概率:
(2)设在该次比赛中,丙得分为ξ,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)甲获第一,则甲胜乙且甲胜丙,丙获第二,则丙胜乙,由此能求出甲获第一名且丙获第二名的概率.(2)ξ的可能取值为0,3,6,分别求出相应的概率之后,由此能求出ξ的分布列和数学期望.
解答:
解:(1)甲获第一,则甲胜乙且甲胜丙,
∴甲获第一的概率为:
×
=
,
丙获第二,则丙胜乙,其概率为1-
=
,
∴甲获第一名且丙获第二名的概率p=
×
=
.
(2)ξ的可能取值为0,3,6,
甲两场比赛全输的概率为:
P(ξ=0)=(1-
)(1-
)=
;
甲两场比赛只胜一场的概率为:
P(ξ=3)=
(1-
)+
(1-
)=
;
甲两场全胜的概率:
P(ξ=6)=
×
=
.
∴ξ的分布列为:
Eξ=0×
+3×
+6×
=
.
∴甲获第一的概率为:
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
丙获第二,则丙胜乙,其概率为1-
| 1 |
| 5 |
| 4 |
| 5 |
∴甲获第一名且丙获第二名的概率p=
| 1 |
| 6 |
| 4 |
| 5 |
| 2 |
| 15 |
(2)ξ的可能取值为0,3,6,
甲两场比赛全输的概率为:
P(ξ=0)=(1-
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
甲两场比赛只胜一场的概率为:
P(ξ=3)=
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 3 |
| 7 |
| 12 |
甲两场全胜的概率:
P(ξ=6)=
| 2 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
∴ξ的分布列为:
| ξ | 0 | 3 | 6 | ||||||
| P |
|
|
|
| 1 |
| 4 |
| 7 |
| 12 |
| 1 |
| 6 |
| 11 |
| 4 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,O为原点,若|FE|=|EP|,则双曲线离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
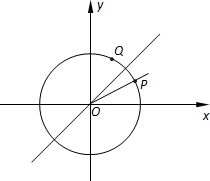 已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=
已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=