题目内容
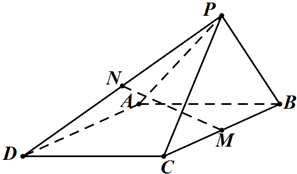 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,∠ABC=60°,△PCB为正三角形,M,N分别为BC,PD的中点.(Ⅰ)求证:MN∥面APB;
(Ⅱ)若平面PCB⊥平面ABCD,求二面角B-NC-P的余弦值.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取AP中点Q,连接NG,MG,由已知条件推导出四边形NQBM为平行四边形,由此能证明MN∥面PAB.
(2)法一:建立空间直角坐标系,得用向量法能求出二面角的余弦值.
(2)法二:连接PM,QM,AM,由已知条件得四边形QNCB为平行四边形,从而推导出∠PNQ为二面角P-NC-B的平面角,由此能求出二面角P-NC-B的余弦值.
(2)法一:建立空间直角坐标系,得用向量法能求出二面角的余弦值.
(2)法二:连接PM,QM,AM,由已知条件得四边形QNCB为平行四边形,从而推导出∠PNQ为二面角P-NC-B的平面角,由此能求出二面角P-NC-B的余弦值.
解答:
(1)证明:取AP中点Q,连接NQ,MQ,
由NQ平行且等于BM,得四边形NQBM为平行四边形,
从而MN∥BQ,∴MN∥面PAB.…(7分)
(2)解法一:建立空间直角坐标系如图,
则有P(0,0,
A(
,0,0),B(0,-1,0),C(0,1,0),D(
,2,0),
由N为PD中点,∴N(
,1,
),…(9分)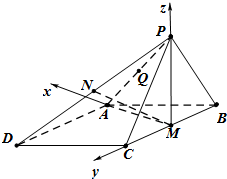
令平面PNC的法向量
=(x, y, z),
由
,令x=-1,则
=(-1,
, 1). …(11分)
同理可知平面BNC的法向量可取
=(
,0,-
)…(13分)
则cos<
,
>=
=-
,
则所求二面角的余弦值为
;…(15分)
(2)解法二:连接PM,QM,AM,
∵NQ∥MC,且NQ=MC,∴四边形QNCB为平行四边形,
∴NQ∥CB且NC∥QM,
∵BC⊥PM,BC⊥AM,∴BC⊥平面PAM,∴BC⊥MQ,即BC⊥NC,
从而NC⊥NQ,又NC⊥NP,
所以∠PNQ为二面角P-NC-B的平面角,
设BC=a,则△PNQ中,NQ=
,NP=
DP=
a,PQ=
PA=
a
所以cos∠PNQ=
=
即二面角P-NC-B的余弦值为
.
由NQ平行且等于BM,得四边形NQBM为平行四边形,
从而MN∥BQ,∴MN∥面PAB.…(7分)
(2)解法一:建立空间直角坐标系如图,
则有P(0,0,
| 3) |
| 3 |
| 3 |
由N为PD中点,∴N(
| ||
| 2 |
| ||
| 2 |

令平面PNC的法向量
| n |
由
|
| n |
| 3 |
同理可知平面BNC的法向量可取
| n2 |
| 3 |
| 3 |
则cos<
| n |
| n2 |
| ||||
|
|
| ||
| 5 |
则所求二面角的余弦值为
| ||
| 5 |
(2)解法二:连接PM,QM,AM,
∵NQ∥MC,且NQ=MC,∴四边形QNCB为平行四边形,
∴NQ∥CB且NC∥QM,
∵BC⊥PM,BC⊥AM,∴BC⊥平面PAM,∴BC⊥MQ,即BC⊥NC,
从而NC⊥NQ,又NC⊥NP,
所以∠PNQ为二面角P-NC-B的平面角,
设BC=a,则△PNQ中,NQ=
| a |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
所以cos∠PNQ=
| NP2+NQ2-PQ2 |
| 2NP•NQ |
| ||
| 5 |
即二面角P-NC-B的余弦值为
| ||
| 5 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
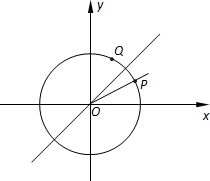 已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=
已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=