题目内容
在无穷数列{an}中,a1=1,对于任意n∈N*,都有an∈N*,an<an+1.设m∈N*,记使得an≤m成立的n的最大值为bm.
(Ⅰ)设数列{an}为1,2,4,10,…,写出b1,b2,b3的值;
(Ⅱ)若{an}是公差为2的等差数列,数列{bm}的前m项的和为Sm,求使得Sm>2014成立的m的最小值;
(Ⅲ)设ap=q,a1+a2+…+ap=A,b1+b2+…+bq=B,请你直接写出B与A的关系式,不需写推理过程.
(Ⅰ)设数列{an}为1,2,4,10,…,写出b1,b2,b3的值;
(Ⅱ)若{an}是公差为2的等差数列,数列{bm}的前m项的和为Sm,求使得Sm>2014成立的m的最小值;
(Ⅲ)设ap=q,a1+a2+…+ap=A,b1+b2+…+bq=B,请你直接写出B与A的关系式,不需写推理过程.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据使得an≤m成立的n的最大值为bm,即可写出b1,b2,b3的值;
(Ⅱ)由an=2n-1≤m,得n≤
.根据bm的定义,当m=2k-1时,bm=k;当m=2k时,bm=k,k∈N*.若m=2k-1,Sm=b1+b2+…+bm=2(1+2+3+…+k-1)+k=k2,由k2>2014的k的最小值为45,得m的最小值为89;若m=2k,Sm=b1+b2+…+bm=2(1+2+3+…+k)=k(k+1),由k(k+1)>2014的k的最小值为45,得m的最小值为90.所以m的最小值为89.
(Ⅲ)由ap=q,a1+a2+…+ap=A,b1+b2+…+bq=B,利用bm的定义能推导出B=p(q+1)-A.
(Ⅱ)由an=2n-1≤m,得n≤
| m+1 |
| 2 |
(Ⅲ)由ap=q,a1+a2+…+ap=A,b1+b2+…+bq=B,利用bm的定义能推导出B=p(q+1)-A.
解答:
(本小题满分14分)
解:(Ⅰ)∵数列{an}为1,2,4,10,…,
使得an≤m成立的n的最大值为bm.
an≤1,则b1=1,an≤2,则b2=2,an≤3,则b3=2.…(3分)
(Ⅱ)∵{an}是公差为2的等差数列,a1=1,
∴an=1+(n-1)×2=2n-1,
由an=2n-1≤m,得n≤
.
根据bm的定义,当m=2k-1时,bm=k;当m=2k时,bm=k,k∈N*.
①若m=2k-1,Sm=b1+b2+…+bm=b1+b2+b3+…+b2k-1
=2(1+2+3+…+k-1)+k=k2,
令k2>2014,由k∈N*,满足k2>2014的k的最小值为45,
则m的最小值为89.…(6分)
②若m=2k,Sm=b1+b2+…+bm=b1+b2+b3+…+b2k
2(1+2+3+…+k)=k(k+1),
令k(k+1)>2014,
由k∈N*满足k(k+1)>2014的k的最小值为45,
则m的最小值为90,…(9分)
由①②知满足Sm>2014的m的最小值为89.…(10分)
(Ⅲ)∵ap=q,a1+a2+…+ap=A,b1+b2+…+bq=B,
∴B=p(q+1)-A.…(14分)
解:(Ⅰ)∵数列{an}为1,2,4,10,…,
使得an≤m成立的n的最大值为bm.
an≤1,则b1=1,an≤2,则b2=2,an≤3,则b3=2.…(3分)
(Ⅱ)∵{an}是公差为2的等差数列,a1=1,
∴an=1+(n-1)×2=2n-1,
由an=2n-1≤m,得n≤
| m+1 |
| 2 |
根据bm的定义,当m=2k-1时,bm=k;当m=2k时,bm=k,k∈N*.
①若m=2k-1,Sm=b1+b2+…+bm=b1+b2+b3+…+b2k-1
=2(1+2+3+…+k-1)+k=k2,
令k2>2014,由k∈N*,满足k2>2014的k的最小值为45,
则m的最小值为89.…(6分)
②若m=2k,Sm=b1+b2+…+bm=b1+b2+b3+…+b2k
2(1+2+3+…+k)=k(k+1),
令k(k+1)>2014,
由k∈N*满足k(k+1)>2014的k的最小值为45,
则m的最小值为90,…(9分)
由①②知满足Sm>2014的m的最小值为89.…(10分)
(Ⅲ)∵ap=q,a1+a2+…+ap=A,b1+b2+…+bq=B,
∴B=p(q+1)-A.…(14分)
点评:本题考查等比数列的性质,考查学生对题意的理解,考查学生分析解决问题的能力,有难度.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
已知函数y=f(x)的导函数y=f′(x)的图象如图,则( )
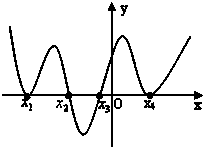

| A、函数f(x)有2个极大值点,2个极小值点 |
| B、函数f(x)有1个极大值点,1个极小值点 |
| C、函数f(x)有3个极大值点,1个极小值点 |
| D、函数f(x)有1个极大值点,3个极小值点. |