题目内容
设f(x)=-x3+x2+2ax.
(1)若f(x)在区间(
,+∞)上存在单调递增区间,求实数a的取值范围;
(2)若函数g(x)=f(x)-2ax+a有且只有一个零点,求实数a的取值范围.
(1)若f(x)在区间(
| 3 |
| 4 |
(2)若函数g(x)=f(x)-2ax+a有且只有一个零点,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)由f′(x)=-3x2+2x+2a,得存在x0∈(
,+∞)使f′(x0)>0,从而f′(
)>0,解出即可;
(2)由g′(x)=-3x2+2x,得x=0时g(x)有极小值=g(0)=a; x=
时g(x)有极大值=g(
)=a+
.从而g(0)=a>0,或g(
)=a+
<0.
| 3 |
| 4 |
| 3 |
| 4 |
(2)由g′(x)=-3x2+2x,得x=0时g(x)有极小值=g(0)=a; x=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 27 |
| 2 |
| 3 |
| 4 |
| 27 |
解答:
解:(1)∵f′(x)=-3x2+2x+2a,
而f(x) 在区间(
,+∞)上存在单调递增区间.
∴存在x0∈(
,+∞)使f′(x0)>0,
又二次函数f′(x)的对称轴为x=
,
则f′(x)在(
,+∞)上递减
∴f′(
)>0,
即-3×
+2×
+2a>0,
故a>
.
(2)∵g(x)=f(x)-2ax+a=-x3+x2+a,
∴g′(x)=-3x2+2x=x(-3x+2)
∴x∈(0,
)时g′(x)>0,g(x)单调递增;
x∈(-∞,0)或(
,+∞)时g′(x)<0,g(x)单调递减.
∴x=0时g(x)有极小值=g(0)=a;
x=
时g(x)有极大值=g(
)=a+
.
∵函数g(x)=f(x)-2ax+a有且只有一个零点,
∴g(0)=a>0,或g(
)=a+
<0
故:a<-
或a>0.
而f(x) 在区间(
| 3 |
| 4 |
∴存在x0∈(
| 3 |
| 4 |
又二次函数f′(x)的对称轴为x=
| 1 |
| 3 |
则f′(x)在(
| 3 |
| 4 |
∴f′(
| 3 |
| 4 |
即-3×
| 9 |
| 16 |
| 3 |
| 4 |
故a>
| 3 |
| 32 |
(2)∵g(x)=f(x)-2ax+a=-x3+x2+a,
∴g′(x)=-3x2+2x=x(-3x+2)
∴x∈(0,
| 2 |
| 3 |
x∈(-∞,0)或(
| 2 |
| 3 |
∴x=0时g(x)有极小值=g(0)=a;
x=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 27 |
∵函数g(x)=f(x)-2ax+a有且只有一个零点,
∴g(0)=a>0,或g(
| 2 |
| 3 |
| 4 |
| 27 |
故:a<-
| 4 |
| 27 |
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=
在x=0处f(x)( )
|
| A、不连续 |
| B、连续,但不可导 |
| C、可导,但导数不连续 |
| D、可导,且导数连续 |
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)作圆x2+y2=a2的切线,切点为E,延长FE交抛物线y2=4cx于点P,O为原点,若|FE|=|EP|,则双曲线离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
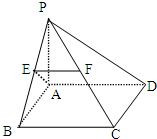 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.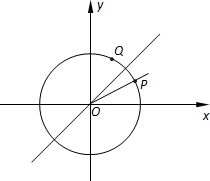 已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=
已知单位圆上两点P、Q关于直线y=x对称,且射线OP为终边的角的大小为x.另有两点M(a,-a)、N(-a,a),且f(x)=