题目内容
已知数列{an}中,a1=2,an+1=2an,
(1)求数列{an}的通项公式及前n项和Sn;
(2)若bn=anlog2an,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式及前n项和Sn;
(2)若bn=anlog2an,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的前n项和
专题:等差数列与等比数列
分析:(1)根据题意判断出数列{an}是等比数列,再代入等比数列的通项公式和前n项和公式化简;
(2)由(1)和条件求出bn,利用错位相减可求{bn}的前n项和Tn.
(2)由(1)和条件求出bn,利用错位相减可求{bn}的前n项和Tn.
解答:
解:(1)由an+1=2an得,
=2,
则数列{an}是以2为首项和公比的等比数列,
∴an=2•2n-1=2n,
Sn=
=2n+1-2
(2)由(1)得,bn=anlog2an=n•2n
∴Tn=1•2+2•22+…+n•2n
2Tn=1•22+2•23+…+(n-1)•2n+n•2n+1
两式相减可得,-Tn=2+22+23+…+2n-n•2n+1
=
-n•2n+1
=(1-n)•2n+1-2
∴Tn=(n-1)•2n+1+2.
| an+1 |
| an |
则数列{an}是以2为首项和公比的等比数列,
∴an=2•2n-1=2n,
Sn=
| 2(1-2n) |
| 1-2 |
(2)由(1)得,bn=anlog2an=n•2n
∴Tn=1•2+2•22+…+n•2n
2Tn=1•22+2•23+…+(n-1)•2n+n•2n+1
两式相减可得,-Tn=2+22+23+…+2n-n•2n+1
=
| 2(1-2n) |
| 1-2 |
=(1-n)•2n+1-2
∴Tn=(n-1)•2n+1+2.
点评:本题考查了等比数列的通项公式、前n项和公式,以及错位相减求数列的和的应用,考查了计算能力.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
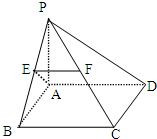 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AP=AB=1,E,F分别是PB,PC的中点.